Question

Let $\alpha_1$, $\alpha_2$ are two values of $\alpha$ for which the system $2\alpha x + y = 5, x - 6y = \alpha$ and $x + y = 2$ is consistent, then $|2(\alpha_1 + \alpha_2)|$ is equal to

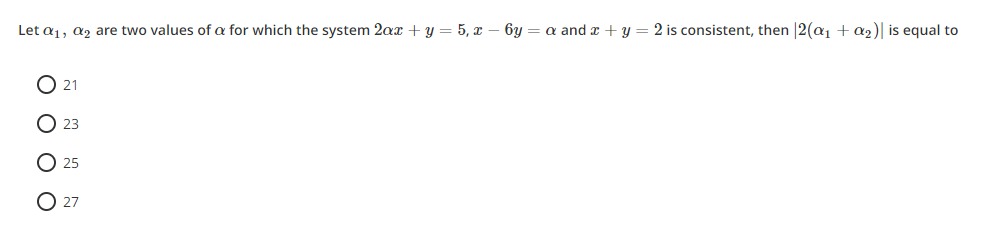
• A. 21
• B. 23
• C. 25
• D. 27

Answer 1

Answer: (B)

23

Answer 2

The system of three linear equations in two variables is consistent if the three lines intersect at a single point.

1. Solve two equations (equations 2 and 3) simultaneously to find the intersection point $(x, y)$ in terms of $\alpha$.
2. Substitute these expressions for $x$ and $y$ into the third equation (equation 1).
3. This results in a quadratic equation in $\alpha$: $2\alpha^2 + 23\alpha - 33 = 0$.
4. The roots of this quadratic equation, $\alpha_1$ and $\alpha_2$, are the values of $\alpha$ for which the system is consistent.
5. Using Vieta's formulas, the sum of the roots $\alpha_1 + \alpha_2 = -\frac{23}{2}$.
6. The required value is $|2(\alpha_1 + \alpha_2)| = |2(-\frac{23}{2})| = |-23| = 23$.