Question
Question: Let $\alpha = \lim_{x \to 0} (\frac{e^x-1}{x})^{\frac{1}{x}}$, $\beta = \lim_{x \to 1} (\ln(ex))^{\l...
Let α=limx→0(xex−1)x1, β=limx→1(ln(ex))logxe and γ=limn→∞n+5nsin(5n)+cos2(2n), then eα2+β+γ is _______.
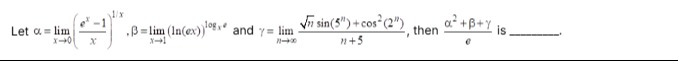
2
Solution
To evaluate the expression eα2+β+γ, we need to calculate the values of α, β, and γ separately.
1. Calculate α=limx→0(xex−1)x1
This limit is of the indeterminate form 1∞. We can evaluate it using the formula limx→a[f(x)]g(x)=elimx→ag(x)[f(x)−1] if limx→af(x)=1 and limx→ag(x)=∞. Here, f(x)=xex−1 and g(x)=x1. As x→0, limx→0xex−1=1 (standard limit) and limx→0x1=∞. So, α=elimx→0x1(xex−1−1). Let's evaluate the exponent L1=limx→0x1(xex−1−x)=limx→0x2ex−1−x. This is of the form 00. We can use L'Hopital's Rule twice or series expansion. Using series expansion: ex=1+x+2!x2+3!x3+O(x4). So, ex−1−x=(1+x+2x2+6x3+O(x4))−1−x=2x2+6x3+O(x4). L1=limx→0x22x2+6x3+O(x4)=limx→0(21+6x+O(x2))=21. Therefore, α=e1/2=e.
2. Calculate β=limx→1(ln(ex))logxe
This limit is also of the indeterminate form 1∞. As x→1, ln(ex)→ln(e⋅1)=lne=1. And logxe=lnxlne=lnx1. As x→1, lnx→0, so lnx1→∞. Let f(x)=ln(ex) and g(x)=logxe. β=elimx→1logxe(ln(ln(ex))). Let's evaluate the exponent L2=limx→1lnx1ln(ln(ex)). We know ln(ex)=lne+lnx=1+lnx. So, L2=limx→1lnxln(1+lnx). Let y=lnx. As x→1, y→0. L2=limy→0yln(1+y). This is a standard limit, which equals 1. Therefore, β=e1=e.
3. Calculate γ=limn→∞n+5nsin(5n)+cos2(2n)
We use the Squeeze Theorem for this limit. We know that −1≤sin(5n)≤1 and 0≤cos2(2n)≤1. So, for the numerator: −n⋅1+0≤nsin(5n)+cos2(2n)≤n⋅1+1. −n≤nsin(5n)+cos2(2n)≤n+1. Now, divide by n+5 (which is positive for large n): n+5−n≤n+5nsin(5n)+cos2(2n)≤n+5n+1. Let's find the limits of the lower and upper bounds as n→∞: limn→∞n+5−n=limn→∞1+5/n−1/n=1+00=0. limn→∞n+5n+1=limn→∞1+5/n1/n+1/n=1+00+0=0. By the Squeeze Theorem, γ=0.
4. Calculate eα2+β+γ
Substitute the values of α, β, and γ: α2=(e)2=e. eα2+β+γ=ee+e+0=e2e=2.
The final answer is 2.
Explanation of the solution:
- Calculate α: The limit is of 1∞ form. Use the property lim[f(x)]g(x)=elimg(x)(f(x)−1). Evaluate the exponent limx→0x2ex−1−x using Taylor series expansion of ex around x=0 up to x2 term. This yields 21. So α=e1/2=e.
- Calculate β: The limit is of 1∞ form. Use the same property as for α. The exponent becomes limx→1lnxln(ln(ex)). Substitute ln(ex)=1+lnx. Let y=lnx. The exponent simplifies to limy→0yln(1+y), which is a standard limit equal to 1. So β=e1=e.
- Calculate γ: Use the Squeeze Theorem. The terms sin(5n) and cos2(2n) are bounded between −1 and 1, and 0 and 1 respectively. This gives bounds for the numerator: −n≤Numerator≤n+1. Divide by n+5 and take limits. Both lower and upper bounds approach 0 as n→∞. Thus, γ=0.
- Final Calculation: Substitute α2=e, β=e, and γ=0 into the expression eα2+β+γ. This gives $\frac{e+e+0}{e} = \frac{2e}{e} = 2.
