Question

Let $\alpha, \beta, \gamma, \delta$ be the roots of $x^4 - x^3 - x^2 - 1 = 0$. Also consider $p(x) = x^6 - x^5 - x^3 - x^2 - x$. Then the value of $p(\alpha) + p(\beta) + p(\gamma) + p(\delta)$ cannot be

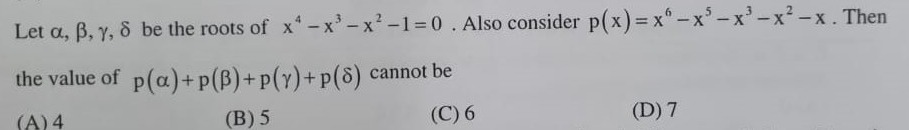
• A. 4
• B. 5
• C. 6
• D. 7

Answer 1

Answer: (C)

6

Answer 2

Let the given polynomial be $f(x) = x^4 - x^3 - x^2 - 1$. The roots of $f(x) = 0$ are $\alpha, \beta, \gamma, \delta$. Thus, for any root $r \in \{\alpha, \beta, \gamma, \delta\}$, we have $r^4 - r^3 - r^2 - 1 = 0$, which implies $r^4 = r^3 + r^2 + 1$.

We are given the polynomial $p(x) = x^6 - x^5 - x^3 - x^2 - x$. We want to evaluate $p(r)$ for a root $r$ of $f(x) = 0$. We can reduce the powers of $r$ using the relation $r^4 = r^3 + r^2 + 1$.

First, let's find $r^5$ and $r^6$ in terms of lower powers of $r$: $r^5 = r \cdot r^4 = r(r^3 + r^2 + 1) = r^4 + r^3 + r$. Substitute $r^4 = r^3 + r^2 + 1$: $r^5 = (r^3 + r^2 + 1) + r^3 + r = 2r^3 + r^2 + r + 1$.

$r^6 = r \cdot r^5 = r(2r^3 + r^2 + r + 1) = 2r^4 + r^3 + r^2 + r$. Substitute $r^4 = r^3 + r^2 + 1$: $r^6 = 2(r^3 + r^2 + 1) + r^3 + r^2 + r = 2r^3 + 2r^2 + 2 + r^3 + r^2 + r = 3r^3 + 3r^2 + r + 2$.

Now substitute the expressions for $r^6$ and $r^5$ into $p(r)$: $p(r) = r^6 - r^5 - r^3 - r^2 - r$ $p(r) = (3r^3 + 3r^2 + r + 2) - (2r^3 + r^2 + r + 1) - r^3 - r^2 - r$ Group terms by powers of $r$: $p(r) = (3 - 2 - 1)r^3 + (3 - 1 - 1)r^2 + (1 - 1 - 1)r + (2 - 1)$ $p(r) = 0r^3 + 1r^2 - 1r + 1$ $p(r) = r^2 - r + 1$.

So, for each root $\alpha, \beta, \gamma, \delta$, we have: $p(\alpha) = \alpha^2 - \alpha + 1$ $p(\beta) = \beta^2 - \beta + 1$ $p(\gamma) = \gamma^2 - \gamma + 1$ $p(\delta) = \delta^2 - \delta + 1$

We need to find the sum $S = p(\alpha) + p(\beta) + p(\gamma) + p(\delta)$. $S = (\alpha^2 - \alpha + 1) + (\beta^2 - \beta + 1) + (\gamma^2 - \gamma + 1) + (\delta^2 - \delta + 1)$ $S = (\alpha^2 + \beta^2 + \gamma^2 + \delta^2) - (\alpha + \beta + \gamma + \delta) + (1 + 1 + 1 + 1)$ $S = \Sigma \alpha^2 - \Sigma \alpha + 4$.

Now, we use Vieta's formulas for the polynomial $f(x) = x^4 - x^3 - x^2 + 0x - 1 = 0$. Sum of roots: $\Sigma \alpha = \alpha + \beta + \gamma + \delta = -(-1)/1 = 1$. Sum of products of roots taken two at a time: $\Sigma \alpha\beta = \alpha\beta + \alpha\gamma + \alpha\delta + \beta\gamma + \beta\delta + \gamma\delta = -1/1 = -1$.

The sum of squares of the roots is given by the formula $\Sigma \alpha^2 = (\Sigma \alpha)^2 - 2 \Sigma \alpha\beta$. $\Sigma \alpha^2 = (1)^2 - 2(-1) = 1 + 2 = 3$.

Substitute these values into the expression for $S$: $S = \Sigma \alpha^2 - \Sigma \alpha + 4$ $S = 3 - 1 + 4$ $S = 2 + 4 = 6$.

The value of $p(\alpha) + p(\beta) + p(\gamma) + p(\delta)$ is 6.