Question
Question: Let $\alpha, \beta$ be roots of $x^2 + \sqrt{2}x - 8 = 0$. If $U_n = \alpha^n + \beta^n$, then $\fra...
Let α,β be roots of x2+2x−8=0. If Un=αn+βn, then 2U8U10+2U9 is equal to ____.
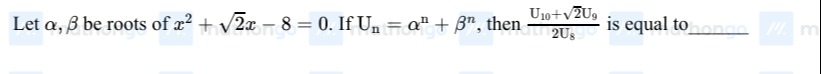
4
Solution
Let α,β be the roots of the quadratic equation x2+2x−8=0. Since α and β are roots of the equation, they must satisfy the equation. Thus, we have: α2+2α−8=0⟹α2+2α=8(1) β2+2β−8=0⟹β2+2β=8(2)
We are given Un=αn+βn. We need to find the value of 2U8U10+2U9.
Substitute the definition of Un into the expression: 2U8U10+2U9=2(α8+β8)(α10+β10)+2(α9+β9)
Expand the numerator: =2(α8+β8)α10+β10+2α9+2β9
Rearrange the terms in the numerator by grouping terms involving α and β: =2(α8+β8)(α10+2α9)+(β10+2β9)
Factor out α8 from the first parenthesis and β8 from the second parenthesis in the numerator: =2(α8+β8)α8(α2+2α)+β8(β2+2β)
Now, substitute the relations from (1) and (2) into this expression: =2(α8+β8)α8(8)+β8(8)
Factor out 8 from the numerator: =2(α8+β8)8(α8+β8)
Since the roots α,β are real and non-zero (as the constant term is -8), α8+β8 will not be zero. Thus, we can cancel the term (α8+β8) from the numerator and denominator: =28 =4
