Question

Let $\alpha$ be the angle between the lines whose direction cosines satisfy the equations $l+m-n=0$ and $l+m^2-n^2=0$. Then the value of $\frac{\sin^4\alpha}{\cos^4\alpha}$ is

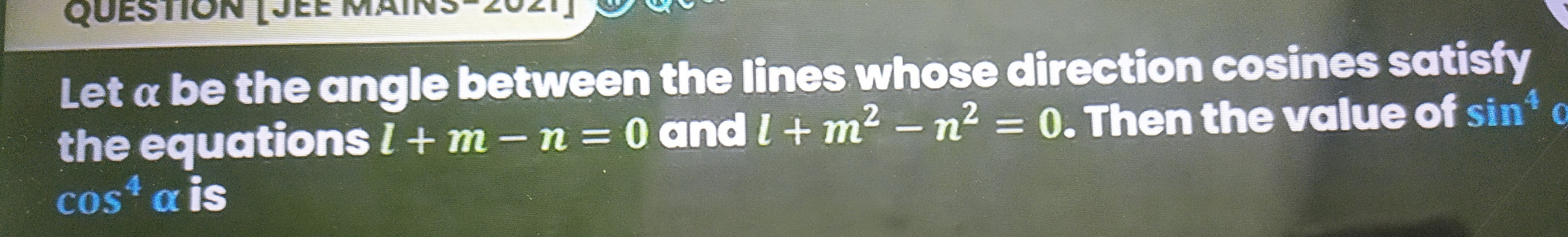
• A. 1
• B. 1/2
• C. 2
• D. 1/4

Answer 1

Answer: (A)

1

Answer 2

The direction cosines $(l, m, n)$ satisfy $l+m-n=0$ and $l+m^2-n^2=0$. From the first equation, $n=l+m$. Substituting this into the second equation: $l+m^2-(l+m)^2=0$ $l+m^2-(l^2+2lm+m^2)=0$ $l-l^2-2lm=0$ $l(1-l-2m)=0$ This implies $l=0$ or $1-l-2m=0$.

Case 1: $l=0$. From $l+m-n=0$, we get $m-n=0 \implies n=m$. Using $l^2+m^2+n^2=1$, we have $0^2+m^2+m^2=1 \implies 2m^2=1 \implies m = \pm \frac{1}{\sqrt{2}}$. This gives direction cosines $(0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ and $(0, -\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}})$, which define one line. Let $\vec{d}_1 = (0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$.

Case 2: $1-l-2m=0 \implies l=1-2m$. From $l+m-n=0$, we get $n=l+m = (1-2m)+m = 1-m$. Using $l^2+m^2+n^2=1$: $(1-2m)^2+m^2+(1-m)^2=1$ $1-4m+4m^2+m^2+1-2m+m^2=1$ $6m^2-6m+2=1$ $6m^2-6m+1=0$. The roots for $m$ are $m = \frac{6 \pm \sqrt{36-24}}{12} = \frac{6 \pm \sqrt{12}}{12} = \frac{6 \pm 2\sqrt{3}}{12} = \frac{3 \pm \sqrt{3}}{6}$. Let $m_1 = \frac{3+\sqrt{3}}{6}$ and $m_2 = \frac{3-\sqrt{3}}{6}$. For $m_1$: $l_1 = 1-2m_1 = 1-2(\frac{3+\sqrt{3}}{6}) = 1-\frac{3+\sqrt{3}}{3} = \frac{3-3-\sqrt{3}}{3} = -\frac{\sqrt{3}}{3} = -\frac{1}{\sqrt{3}}$. $n_1 = 1-m_1 = 1-\frac{3+\sqrt{3}}{6} = \frac{6-3-\sqrt{3}}{6} = \frac{3-\sqrt{3}}{6}$. So, $\vec{d}_2 = (-\frac{1}{\sqrt{3}}, \frac{3+\sqrt{3}}{6}, \frac{3-\sqrt{3}}{6})$. For $m_2$: $l_2 = 1-2m_2 = 1-2(\frac{3-\sqrt{3}}{6}) = 1-\frac{3-\sqrt{3}}{3} = \frac{3-3+\sqrt{3}}{3} = \frac{\sqrt{3}}{3} = \frac{1}{\sqrt{3}}$. $n_2 = 1-m_2 = 1-\frac{3-\sqrt{3}}{6} = \frac{6-3+\sqrt{3}}{6} = \frac{3+\sqrt{3}}{6}$. So, $\vec{d}_3 = (\frac{1}{\sqrt{3}}, \frac{3-\sqrt{3}}{6}, \frac{3+\sqrt{3}}{6})$.

The problem implies there are two lines. The most natural interpretation is that the two lines are $\vec{d}_2$ and $\vec{d}_3$ derived from $1-l-2m=0$. Let's find the angle $\alpha$ between $\vec{d}_2$ and $\vec{d}_3$. $\cos \alpha = |\vec{d}_2 \cdot \vec{d}_3| = |(-\frac{1}{\sqrt{3}})(\frac{1}{\sqrt{3}}) + (\frac{3+\sqrt{3}}{6})(\frac{3-\sqrt{3}}{6}) + (\frac{3-\sqrt{3}}{6})(\frac{3+\sqrt{3}}{6})|$ $\cos \alpha = |-\frac{1}{3} + \frac{9-3}{36} + \frac{9-3}{36}| = |-\frac{1}{3} + \frac{6}{36} + \frac{6}{36}| = |-\frac{1}{3} + \frac{1}{6} + \frac{1}{6}| = |-\frac{1}{3} + \frac{1}{3}| = 0$. This means $\alpha = \frac{\pi}{2}$. If $\alpha = \frac{\pi}{2}$, then $\sin\alpha=1$ and $\cos\alpha=0$. The expression $\frac{\sin^4\alpha}{\cos^4\alpha}$ is undefined.

Alternatively, if the two lines are $\vec{d}_1$ and $\vec{d}_2$ (or $\vec{d}_1$ and $\vec{d}_3$). Let's find the angle $\alpha$ between $\vec{d}_1$ and $\vec{d}_2$. $\cos \alpha = |\vec{d}_1 \cdot \vec{d}_2| = |(0)(-\frac{1}{\sqrt{3}}) + (\frac{1}{\sqrt{2}})(\frac{3+\sqrt{3}}{6}) + (\frac{1}{\sqrt{2}})(\frac{3-\sqrt{3}}{6})|$ $\cos \alpha = |\frac{1}{\sqrt{2}}(\frac{3+\sqrt{3}+3-\sqrt{3}}{6})| = |\frac{1}{\sqrt{2}}(\frac{6}{6})| = \frac{1}{\sqrt{2}}$. So, $\alpha = \frac{\pi}{4}$. Then $\sin \alpha = \frac{1}{\sqrt{2}}$ and $\cos \alpha = \frac{1}{\sqrt{2}}$. $\frac{\sin^4\alpha}{\cos^4\alpha} = \frac{(1/\sqrt{2})^4}{(1/\sqrt{2})^4} = 1$. This matches one of the options and avoids an undefined result.