Question

Let $\alpha$ and $\beta$ are roots of $x^2 - 17x - 6 = 0$ with $\alpha > \beta$. If $a_n = \alpha^n + \beta^n$. The value of $\frac{a_{10} - 6a_8}{a_9}$ is _______.

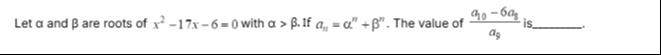
Answer 1

17

Answer 2

Given that $\alpha$ and $\beta$ are roots of $x^2-17x-6=0$, we have

$\alpha+\beta=17$ and $\alpha\beta=-6$.

Since $\alpha$ is a root, it satisfies: $\alpha^2-17\alpha-6=0 \Rightarrow \alpha^2=17\alpha+6$.

Subtract 6 from both sides: $\alpha^2-6=17\alpha$.

Multiply this by $\alpha^8$: $\alpha^8(\alpha^2-6)=17\alpha^9 \Rightarrow \alpha^{10}-6\alpha^8=17\alpha^9$.

Similarly, for $\beta$: $\beta^{10}-6\beta^8=17\beta^9$.

Now, $a_n=\alpha^n+\beta^n$. Therefore, $a_{10}-6a_8=(\alpha^{10}+\beta^{10})-6(\alpha^8+\beta^8) =[\alpha^{10}-6\alpha^8]+[\beta^{10}-6\beta^8]=17\alpha^9+17\beta^9=17(\alpha^9+\beta^9)=17a_9$.

Thus, $\frac{a_{10}-6a_8}{a_9}=\frac{17a_9}{a_9}=17$.