Solveeit Logo
Login

Question

Question: Let ABCDEF be a regular hexagon in the x – y plane and \(\vec A\vec B = 4\hat i\), then \(\vec C\vec...

Let ABCDEF be a regular hexagon in the x – y plane and A⃗B⃗=4i^\vec A\vec B = 4\hat i, then C⃗D⃗\vec C\vec D is equal to
(a)6i^+23j^\left( a \right)6\hat i + 2\sqrt 3 \hat j
(b)2(−i^+3j^)\left( b \right)2\left( { - \hat i + \sqrt 3 \hat j} \right)
(c)2(i^+3j^)\left( c \right)2\left( {\hat i + \sqrt 3 \hat j} \right)
(d)2(i^−3j^)\left( d \right)2\left( {\hat i - \sqrt 3 \hat j} \right)

Explanation

Solution

In this particular question use the concept that in a regular hexagon the length of all sides is the equal only difference is the direction assume AB be the reference direction i.e. AB on the positive x-axis and use the concept that the internal angle of a regular hexagon is always 120 degrees, so use these concepts to reach the solution of the question.

Complete step-by-step solution:
__
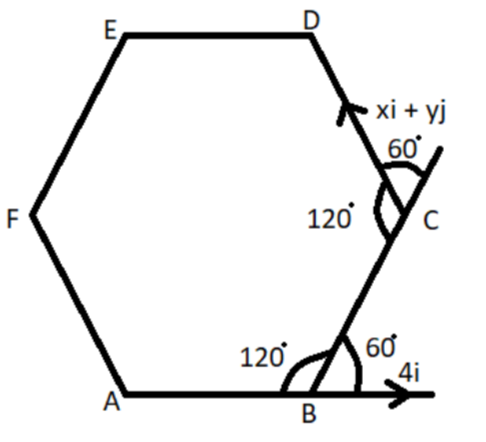
ABCDEF regular hexagon is shown above in the diagram.
Let AB be the reference, and it is given that A⃗B⃗=4i^\vec A\vec B = 4\hat i
Now we have to find out the C⃗D⃗\vec C\vec D as shown in the above figure.
Let, C⃗D⃗=xi^+yj^\vec C\vec D = x\hat i + y\hat j
Now as we know that in a regular hexagon the length of all sides is equal i.e. magnitude of the sides is equal.
⇒∣A⃗B⃗∣=∣C⃗D⃗∣\Rightarrow \left| {\vec A\vec B} \right| = \left| {\vec C\vec D} \right|
⇒∣4i^∣=∣xi^+yj^∣\Rightarrow \left| {4\hat i} \right| = \left| {x\hat i + y\hat j} \right|
Now as we know that ∣xi^+yj^∣=x2+y2\left| {x\hat i + y\hat j} \right| = \sqrt {{x^2} + {y^2}} so use this property in the above equation we have,
⇒42+02=x2+y2\Rightarrow \sqrt {{4^2} + {0^2}} = \sqrt {{x^2} + {y^2}}
Now take square root on both sides we have,
⇒42=x2+y2\Rightarrow {4^2} = {x^2} + {y^2}..................... (1)
Now as we know that the internal angle of a regular hexagon is always 120 degrees as shown in the above figure.
⇒∠ABC=120o\Rightarrow \angle ABC = {120^o}
So the angle line BC makes with the positive direction of x axis is,
⇒180o−120o=60o\Rightarrow {180^o} - {120^o} = {60^o}
So the line CD makes an angle (60o+60o)=120o\left( {{{60}^o} + {{60}^o}} \right) = {120^o} with the positive direction of x axis.
So the slope of the line CD is, tan⁡120o=−3\tan {120^o} = - \sqrt 3 .............. (2)
But, C⃗D⃗=xi^+yj^\vec C\vec D = x\hat i + y\hat j
And the slope of the above equation is,
tan⁡θ=yx\tan \theta = \dfrac{y}{x}................ (3)
Now (2) and (3) both are the same so equate them we have,
⇒yx=−3\Rightarrow \dfrac{y}{x} = - \sqrt 3
⇒y=−x3\Rightarrow y = - x\sqrt 3............... (4)
Now substitute this value in equation (1) we have,
⇒42=x2+(−x3)2\Rightarrow {4^2} = {x^2} + {\left( { - x\sqrt 3 } \right)^2}
⇒42=x2+3x2\Rightarrow {4^2} = {x^2} + 3{x^2}
⇒4x2=16\Rightarrow 4{x^2} = 16
⇒x2=4\Rightarrow {x^2} = 4
⇒x=±2\Rightarrow x = \pm 2
Now as the direction of the line CD is 120 degrees with the positive direction of the x-axis so the line lies in the second quadrant, and in the second quadrant x is negative and y is positive.
Therefore, x = -2
Now substitute this value in equation (4) we have,
⇒y=23\Rightarrow y = 2\sqrt 3
So the vector CD becomes
⇒C⃗D⃗=−2i^+23j^=2(−i^+3j^)\Rightarrow \vec C\vec D = - 2\hat i + 2\sqrt 3 \hat j = 2\left( { - \hat i + \sqrt 3 \hat j} \right)
So this is the required vector.
Hence option (b) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that after 120-degree rotation with the reference in anti-clockwise the vector goes into the second quadrant and in the second quadrant the value of x is negative and the value of y is positive so chose the values of x and y during calculation according to this as above chosen.