Question

Let ABCD is parallelogram such that $\overline {AB} = \overrightarrow q ,\overline {AD} = \overrightarrow p {\text{ and }}\angle BAD$ be an acute angle. If $\overrightarrow r$ is the vector coincides with the altitude directed from the vertex $B$ to the side $AD$, then $\overrightarrow r$ is given by:

$${\text{(A) }}\overrightarrow r = 3\overrightarrow q - \dfrac{{3(\overrightarrow p .\overrightarrow q )}}{{\overrightarrow p .\overrightarrow p }}\overrightarrow p \\\ {\text{(B) }}\overrightarrow r = - \overrightarrow q + \left( {\dfrac{{\overrightarrow p .\overrightarrow q }}{{\overrightarrow p .\overrightarrow p }}} \right)\overrightarrow p \\\ {\text{(C) }}\overrightarrow r = \overrightarrow q - \left( {\dfrac{{\overrightarrow p .\overrightarrow q }}{{\overrightarrow p .\overrightarrow p }}} \right)\overrightarrow p \\\ {\text{(D) }}\overrightarrow r = - 3\overrightarrow q + \dfrac{{3(\overrightarrow p .\overrightarrow q )}}{{\overrightarrow p .\overrightarrow p }}\overrightarrow p \\\$$

Answer 1

This problem is related to vector geometry. It should be noted here that a dot product of two vectors is a scalar quantity ($\overrightarrow A .\overrightarrow B = AB\cos \theta ,$ where $\theta$ is the angle between them) and if the vectors are perpendicular to each other their dot product is zero because the value of $\cos {90^ \circ } = 0$. We will use this property of vector products to solve the problem.

Complete step-by-step answer:
Firstly, draw a parallelogram ABCD in such a way that $\overline {AB} = \overrightarrow q ,\overline {AD} = \overrightarrow p {\text{ and }}\angle BAD$ should be an acute angle. See below,

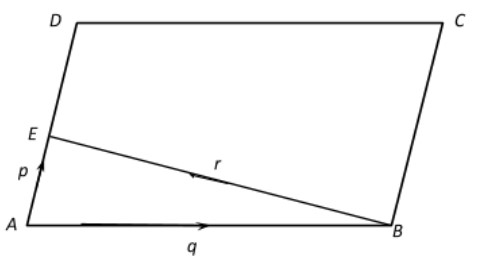
Now, in the diagram, draw a line originating from vertex $B$ to the side $AD$ in such a way that it should be perpendicular to side $AD$. This way $\Delta AEB$ will be a right angle triangle.
We know that, vector$\overrightarrow r$can be written in the form of vector $\overrightarrow q$ and vector $\overrightarrow p$. Now, from the diagram above, it is known that the direction of vector $\overrightarrow r$is opposite to the direction of vector$\overrightarrow q$. Hence, when we write the vector $\overrightarrow r$ in terms of vector $\overrightarrow q$, we shall have to put a negative sign in front of the vector $\overrightarrow q$.
Now, vector $\overrightarrow p$represents the side $AD$, so assume that $\alpha \overrightarrow p$represents the side $AE$ in $\Delta AEB$. Therefore, now vector $\overrightarrow r$can be written in the form of vector $\overrightarrow q$ and vector $\overrightarrow p$ in the following way,
$\overrightarrow r = - \overrightarrow q + \alpha \overrightarrow p {\text{ }}................(1)$
Now, we know that the dot product to two perpendicular vectors is zero. In this diagram, vector$\overrightarrow r$and vector$\overrightarrow p$ are perpendicular to each other.
Therefore,
$\overrightarrow r .\overrightarrow p = 0$
Putting the value of vector$\overrightarrow r$ from eq. (1) in the above expression, we will get

$$\overrightarrow r .\overrightarrow p = 0 \\\ \Rightarrow ( - \overrightarrow q + \alpha \overrightarrow p ).\overrightarrow p = 0 \\\ \Rightarrow - \overrightarrow q .\overrightarrow p + \alpha \overrightarrow p .\overrightarrow p = 0 \\\ \Rightarrow \alpha = \dfrac{{\overrightarrow q .\overrightarrow p }}{{\overrightarrow p .\overrightarrow p }} \\\$$

Now, putting this value of $\alpha$, we will get the value of vector$\overrightarrow r$as
$\overrightarrow r = - \overrightarrow q + \dfrac{{\overrightarrow q .\overrightarrow p }}{{\overrightarrow p .\overrightarrow p }}\overrightarrow p$

So, the correct answer is “Option B”.

Note: In these types of problems, you should take care while drawing the diagram and putting the vector’s direction. Though, it is not given in the problem that the vector $\overrightarrow r$is perpendicular to$\overrightarrow p$but we have assumed that they are perpendicular to each other so that property of dot product of vectors can be utilised.