Question

Let ABCD be a square of side length 2 units. A line $m$ through A is drawn parallel to BD. Point S moves such that its distances from the line BD and the vertex A are equal. If locus of S cuts $m$ at ${{T}_{2}}$ and ${{T}_{3}}$ and AC at ${{T}_{1}}$, then area of $\Delta {{T}_{1}}{{T}_{2}}{{T}_{3}}$ in square unit is – $$$$
A. \dfrac{1}{2}$$$$$ B. \dfrac{2}{3} C. $1
D. $2$$$$$

Answer 1

We know that when a point moves such that its distance from a fixed point is equal to its distance from a fixed line, then its locus is a parabola whose directrix is the fixed-line and the fixed point is the focus. Here the locus of S is a parabola with focus A, directrix BD, ${{T}_{1}}$ is the vertex, ${{T}_{2}}{{T}_{3}}$. We find the distance between focus and vertex $a=A{{T}_{1}}$ which also the height of $\Delta {{T}_{1}}{{T}_{2}}{{T}_{3}}$ and then latus rectum ${{T}_{2}}{{T}_{3}}=4a$ which is the base of $\Delta {{T}_{1}}{{T}_{2}}{{T}_{3}}$. We use the formula of the area with base and height. $$$$

Complete step-by-step solution

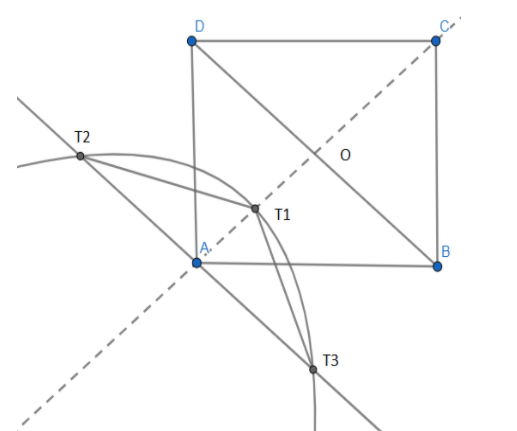
We have drawn the required figure as given in the question. The square is ABCD with length 2 units which mean $AB=BC=CD=DA=2$units. We denote the point of intersection of the diagonals BD and AC as O. We use the Pythagoras theorem in the triangle BAO and find the length of semi-diagonal as

& A{{O}^{2}}+O{{B}^{2}}=A{{B}^{2}} \\\ & \Rightarrow 2A{{O}^{2}}={{2}^{2}}\left( \because AO=OB \right) \\\ & \Rightarrow AO=\sqrt{2} \\\ \end{aligned}$$ The line $m$ is drawn parallel to BD. The point S moves in a way such that its distances from the line BD and the vertex A are equal. We know that when a point moves such that its distance from a fixed point is equal to its distance from a fixed line, then its locus is a parabola whose directrix is the fixed-line and the fixed point is the focus. So here the fixed point A is the focus, the fixed-line BD is the directrix, and the locus of is the parabola. The line through focus and perpendicular to directrix called axis which here is OA .$$$$ We are further given that the locus of S cuts $m$ at ${{T}_{2}}$ and ${{T}_{3}}$ and AC at ${{T}_{1}}$. As ${{T}_{1}}$ a point on the parabola is equidistant from A and BD we have $A{{T}_{1}}={{T}_{1}}O$ $$\begin{aligned} & A{{T}_{1}}+{{T}_{1}}O=AO \\\ & \Rightarrow 2A{{T}_{1}}=\sqrt{2}\left( \because A{{T}_{1}}={{T}_{1}}O \right) \\\ & \Rightarrow A{{T}_{1}}=\dfrac{1}{\sqrt{2}} \\\ \end{aligned}$$ The point of intersection of parabola and axis is called vertex which here is ${{T}_{1}}.$We know from the standard equation of parabola in vertex form ${{y}^{2}}=4ax$ that $a$ is the distance between focus and vertex. So we have $$a=A{{T}_{1}}=\dfrac{1}{\sqrt{2}}$$ We also know that ${{T}_{2}}{{T}_{3}}$ is called the latus rectum of the parabola whose length is given by $${{T}_{2}}{{T}_{3}}=4a=4\left( \dfrac{1}{\sqrt{2}} \right)$$ So the area $\Delta $ of the triangle ${{T}_{1}}{{T}_{2}}{{T}_{3}}$ with base ${{T}_{2}}{{T}_{3}}$ and height $A{{T}_{1}}$ is $$\Delta =\dfrac{1}{2}\times {{T}_{2}}{{T}_{3}}\times A{{T}_{1}}=\dfrac{1}{2}\times 4\left( \dfrac{1}{\sqrt{2}} \right)\times \dfrac{1}{\sqrt{2}}=1$$ **So area of the triangle ${{T}_{1}}{{T}_{2}}{{T}_{3}}$ is 1 square unit and hence correct option is C.** **Note:** We note that we can also find ${{T}_{2}}{{T}_{3}}$ using the coordinates of endpoints of latus rectum $\left( a,2a \right),\left( a,-2a \right)$. Circle does not have a latus rectum. The length of latus rectum of the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is $\dfrac{2{{b}^{2}}}{a}$ if $a>b$ and $\dfrac{2{{a}^{2}}}{b}$ if $b>a.$ The length of latus rectum of hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is $\dfrac{2{{b}^{2}}}{a}$.