Question

Let ABCD be a quadrilateral with area $18$ , with side AB parallel to the side CD and $AB=2CD$ . Let AD be the perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is
A. $3$
B. $2$
C. $\dfrac{3}{2}$
D. $1$

Answer 1

Hint : In order to solve the question, first by using the area of the quadrilateral and substituting the values we get the relation between the side and the radius i.e. $\alpha =\dfrac{6}{r}$ . Then we know that the line BC is tangent to the circle, the equation of the circle is given by ${{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}$ . Then by calculating the perpendicular distance of BC from the centre by equating it with the radius. Simplifying this will give you the required value of the radius.
Formula used:
The area of the quadrilateral is given by;
$\dfrac{1}{2}\times base\times height$
The equation of the circle is given by:
${{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}$

Complete step-by-step answer :
We have given that,
The ABCD is a quadrilateral with area $18$ , with side AB parallel to the side CD and $AB=2CD$ . Let AD be the perpendicular to AB and CD.
Let the circle be of the radius ‘r’.
And
Height of the quadrilateral = $2\times r=2r$ (here ‘r’ is the radius)
According to the information given above in the question, we need to draw figure,
The figure of the quadrilateral is as follows;

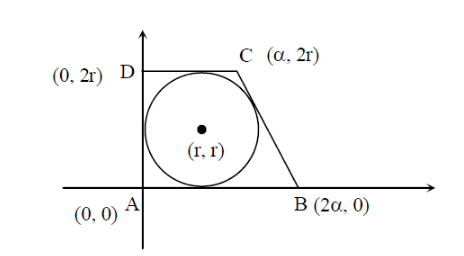
As we know that,
The area of quadrilateral = $\dfrac{1}{2}\times base\times height$
In the given question,
Area of the quadrilateral = $18$
Height of the quadrilateral = $2\times r=2r$ (here ‘r’ is the radius)
Base of the quadrilateral = $\alpha +2\alpha =3\alpha$
Therefore,
$\Rightarrow 18=\dfrac{1}{2}\times 3\alpha \times 2r$
$\Rightarrow \alpha r=6$
$\Rightarrow \alpha =\dfrac{6}{r}$ -------- (1)
Now,
The equation of the line BC is given by;
$y=-\dfrac{2r}{\alpha }\left( x-2\alpha \right)$
The line BC is tangent to the circle given by;
${{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}$
Therefore,
Perpendicular distance of BC from the centre is equal to radius.
$\Rightarrow \dfrac{\left| r+\dfrac{2r}{\alpha }\left( r-2\alpha \right) \right|}{\sqrt{1+\dfrac{4{{r}^{2}}}{{{\alpha }^{2}}}}}=r$
Simplifying the above, we will get
$\Rightarrow \left| r+\dfrac{2r}{\alpha }\left( r-2\alpha \right) \right|=r\sqrt{1+\dfrac{4{{r}^{2}}}{{{\alpha }^{2}}}}$
Simplifying the LHS of the above equation,
$\Rightarrow r+\dfrac{2{{r}^{2}}}{\alpha }-4r=r\sqrt{1+\dfrac{4{{r}^{2}}}{{{\alpha }^{2}}}}$
Combining the like terms, we will get
$\Rightarrow \dfrac{2{{r}^{2}}}{\alpha }-3r=r\sqrt{1+\dfrac{4{{r}^{2}}}{{{\alpha }^{2}}}}$
Simplifying further,
$\Rightarrow {{\left( 2r-3\alpha \right)}^{2}}={{\alpha }^{2}}+4{{r}^{2}}$
$\Rightarrow r\cdot \alpha =\dfrac{2}{3}{{\alpha }^{2}}$
$\Rightarrow 3r=2\alpha$ ------ (2)
From the equation (1) and equation (2),
Putting the value of equation (1) in equation (2)
$\Rightarrow 3r=2\left( \dfrac{6}{r} \right)=\dfrac{12}{r}$
$\Rightarrow 3{{r}^{2}}=12$
Dividing both the sides of the equation by 3,
$\Rightarrow {{r}^{2}}=4$
$\Rightarrow r=\sqrt{4}=\pm 2$
As we know that the value of radius can never be negative.
Therefore,
$\Rightarrow r=2\;units$
So, the radius of the circle is 2 units.
So, the correct answer is “Option B”.

Note : Students here need to note that the length of the side AD is equal to the twice of the radius ‘r’. The side AD of the quadrilateral is perpendicular to the side AB and CD. So the length AD becomes the distance between the two sides and also becomes the diameter of the circle and dividing it by 2 we get the required value of the radius.