Question

Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10 cm and 20 cm, respectively. If the angle $∠ADC$ is equal to 30° then the area of the parallelogram, in sq. cm, is

• A. $\frac{25(\sqrt{3}+\sqrt{15})}{2}$
• B. $25(\sqrt5+\sqrt{15})$
• C. $\frac{25(\sqrt5+\sqrt{15})}{2}$
• D. $25(\sqrt3+\sqrt{15})$

Answer 1

Answer: (D)

$25(\sqrt3+\sqrt{15})$

Answer 2

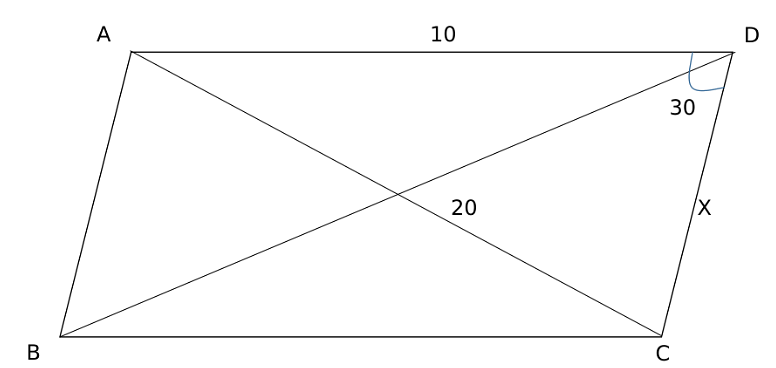
Applying cosine rule in triangle ACD
$100+X ^2 −2× 10× Xcos30=400$
$X^ 2 −10X \sqrt3−300=0$

$⇒ X = ( \frac{10\sqrt3 + 10\sqrt{15}}{ 2} )$

X is the length of one of the sides of the parallelogram, hence it can’t be negative.

$∴ area = 10Xsin 30 =\frac{ (\frac{ 10\sqrt3 + 10\sqrt{15} }{2} )10 }{2}$

$= 25 ( \sqrt3 + \sqrt{15} )$