Question

Let ABCD be a parallelogram, if $F$is the midpoint of $AB$ and $DF$ intersects $AC$ at M,$$$\overrightarrow a = \overrightarrow i + \overrightarrow j + 3\overrightarrow {k,} $$$\overrightarrow c = \overrightarrow i + \overrightarrow j where $\overrightarrow a$ and $\overrightarrow c$ are position vector of $A$ and $C$ respectively, which of the following is/are correct.
$\left( {\text{A}} \right)$Position vector of $M$is $\overrightarrow i + \overrightarrow j + 2\overrightarrow k$
$\left( {\text{B}} \right)$Position vector of M is $\overrightarrow i + \overrightarrow j + \overrightarrow k$
\left( {\text{C}} \right)$$$DM:MF = 2:1$ \left( {\text{D}} \right)$$$DM:MF = 1:2$

Answer 1

First we have to use the position of the vector formula instead of finding out the ratio using the given terms.
Then we substitute the value in the formula.
Finally we get the required answer.

Formula used:
Position vector formula: $\dfrac{{m\overrightarrow b + n\overrightarrow a }}{{m + n}}$

Complete step-by-step answer:
For solving the question we need to draw the diagram of the parallelogram for better understanding.

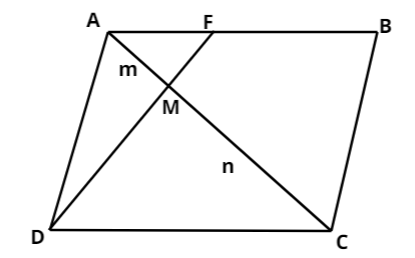
It is given in the question that $F$ is the midpoint of $AB$ and $DF$ intersects $AC$ at the point $M$.
Since the point $M$ divides $AC$ in the ratio of $1:2$, therefore we have $m = 1$and $n = 2$which is equivalent to the value of $AM$ and $MC$.
Now applying position vector formula that is $\dfrac{{m\overrightarrow b + n\overrightarrow a }}{{m + n}}$we get the position vector of
$\overrightarrow M$=$\dfrac{{m\overrightarrow a + n\overrightarrow c }}{{m + n}}$
It is given in the question that the value of $\overrightarrow a = \overrightarrow i + \overrightarrow j + 3\overrightarrow {k,}$and $\overrightarrow c = \overrightarrow i + \overrightarrow j$
Here $m\overrightarrow a + n\overrightarrow c = 1\left( {\overrightarrow i + \overrightarrow j + 3\overrightarrow k } \right) + 2\left( {\overrightarrow i + \overrightarrow j } \right)$
We have to multiply on it, that is we can write it as the form,
$m\overrightarrow a + n\overrightarrow c = \overrightarrow i + \overrightarrow j + 3\overrightarrow k + 2\overrightarrow i + 2\overrightarrow j$
Substitute the above in the formula we get,
Therefore we can write,
$\Rightarrow$ $\overrightarrow M = \dfrac{{\overrightarrow i + \overrightarrow j + 3\overrightarrow k + 2\overrightarrow i + 2\overrightarrow j }}{{1 + 2}}$
Now by adding we get-
$\Rightarrow$ $\overrightarrow M = \dfrac{{3\overrightarrow j + 3\overrightarrow k + 3\overrightarrow i }}{3}$
Taking $3$ as common we get-
$\Rightarrow$ $\overrightarrow M = \dfrac{{3(\overrightarrow j + \overrightarrow k + \overrightarrow i )}}{3}$
Now $3$ will get cancelled and we get-
$\Rightarrow$ $\overrightarrow M = \overrightarrow i + \overrightarrow j + \overrightarrow k$
Therefore it is proved that position vector of $\overrightarrow M = \overrightarrow i + \overrightarrow j + \overrightarrow k$

Hence option B is correct.

Note: This position vector formula $\overrightarrow r = \dfrac{{m\overrightarrow b + n\overrightarrow a }}{{m + n}}$ will be applied when a line divides internally but in case the line divides externally then the formula of finding position vector will be $\overrightarrow r = \dfrac{{m\overrightarrow b - n\overrightarrow a }}{{m - n}}$.
So try to keep this in your mind because many of us make mistakes in such questions.
The opposite sides of a parallelogram are equal and parallel. Their opposites sides and opposite angles are always congruent.
Their diagonals always bisect each other and the diagonals divide the parallelogram into two similar triangles.