Solveeit Logo
Login

Question

Question: Let \(ABC\) is an equilateral triangle of side \[10m\] and \(D\) is the midpoint of \(BC\) . Charges...

Let ABCABC is an equilateral triangle of side 10m10m and DD is the midpoint of BCBC . Charges of +100,−100 and +75μC + 100, - 100{\text{ and }} + 75\mu C bs are placed at B,C,DB,C,D respectively. Find the force on a +1μC + 1\mu C charge placed atAA . (Give your answer in S.I. unit).

Explanation

Solution

To solve this question firstly we will draw the figure and simplify the forces on +1μC + 1\mu C . We will calculate the net electric field along the x-axis and then net field of point AA , after net force acting on the point charger of +1μC + 1\mu C .

Formula used:
E=kqr2E = \dfrac{{kq}}{{{r^2}}}
⇒F=qE\Rightarrow F = qE
Where, EE is the electric field strength,k=9×109k = 9 \times {10^9} is the electrostatic constant,qq is the charge, rr is the distance to the charge creating the field and FF is the force.

Complete step by step answer:

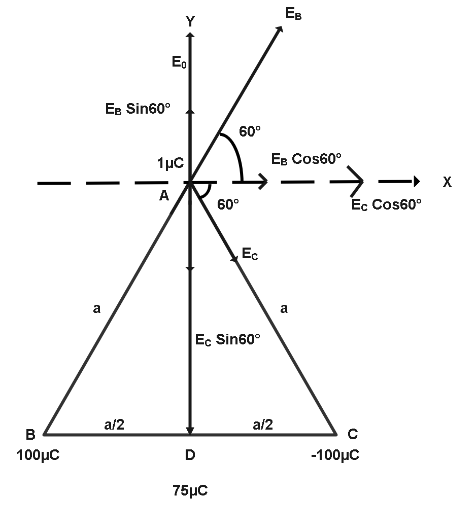
Now, we will calculate net field along -axis at point AA
E(x)=E(B)Cos⁡60∘+E(C)Cos⁡60∘ ⇒E(y)=E(D)+E(B)Sin⁡60∘−E(C)Sin⁡60∘E(x) = E(B)\operatorname{Cos} {60^ \circ } + E(C)\operatorname{Cos} {60^ \circ } \\\ \Rightarrow E(y) = E(D) + E(B)\operatorname{Sin} {60^ \circ } - E(C)\operatorname{Sin} {60^ \circ }
Given that,
a=10ma = 10m
⇒Q(A)=1μC\Rightarrow Q(A) = 1\mu C
⇒Q(B)=100μC\Rightarrow Q(B) = 100\mu C
⇒Q(C)=−100μC\Rightarrow Q(C) = - 100\mu C
⇒Q(D)=75μC\Rightarrow Q(D) = 75\mu C
⇒k=9×109NM2 C−2\Rightarrow k = 9 \times {10^9}N{M^2}{\text{ }}{C^{ - 2}}
Now electric field at AA
∵EA=kQAa2 ⇒EA=9×109×100×10−6102 ⇒EA=9000N C−1 \because {E_A} = k\dfrac{{{Q_A}}}{{{a^2}}} \\\ \Rightarrow {E_A} = 9 \times {10^9} \times \dfrac{{100 \times {{10}^{ - 6}}}}{{{{10}^2}}} \\\ \Rightarrow {E_A} = 9000N{\text{ }}{C^{ - 1}} \\\
Now, electric field at BB is E(B)E(B)
∵EB=kQBa2 ⇒EB=9×109×100×10−6102 ⇒EB=9000N C−1 \because {E_B} = k\dfrac{{{Q_B}}}{{{a^2}}} \\\ \Rightarrow {E_B} = 9 \times {10^9} \times \dfrac{{100 \times {{10}^{ - 6}}}}{{{{10}^2}}} \\\ \Rightarrow {E_B} = 9000N{\text{ }}{C^{ - 1}} \\\
Now,electric field at DD is E(D)E(D)
∵ED=kQDa2 ⇒ED=9×109×75×10−63×1024 ⇒ED=900×10(9−6−2) ⇒ED=9000N C−1 \because {E_D} = k\dfrac{{{Q_D}}}{{{a^2}}} \\\ \Rightarrow {E_D} = 9 \times {10^9} \times \dfrac{{75 \times {{10}^{ - 6}}}}{{\dfrac{{3 \times {{10}^2}}}{4}}} \\\ \Rightarrow {E_D} = 900 \times {10^{(9 - 6 - 2)}} \\\ \Rightarrow {E_D} = 9000N{\text{ }}{C^{ - 1}} \\\
So,
E(x)=9000cos⁡60∘+9000cos⁡60∘ ⇒E(x)=(9000×12)×2 ⇒E(x)=9000N C−1 E(x) = 9000\cos {60^ \circ } + 9000\cos {60^ \circ } \\\ \Rightarrow E(x) = \left( {9000 \times \dfrac{1}{2}} \right) \times 2 \\\ \Rightarrow E(x) = 9000N{\text{ }}{C^{ - 1}} \\\
Now,
E(y)=9000+9000cos⁡60∘+9000cos⁡60∘ ⇒E(y)=9000N C−1 E(y) = 9000 + 9000\cos {60^ \circ } + 9000\cos {60^ \circ } \\\ \Rightarrow E(y) = 9000N{\text{ }}{C^{ - 1}} \\\
So, net electric field at AA
En=Ex2+Ey2 ⇒En=(9000)2+(9000)2 ⇒En=90002 ⇒En=12727.9N C−1 {E_n} = \sqrt {E_x^2 + E_y^2} \\\ \Rightarrow {E_n} = \sqrt {{{(9000)}^2} + {{(9000)}^2}} \\\ \Rightarrow {E_n} = 9000\sqrt 2 \\\ \Rightarrow {E_n} = 12727.9N{\text{ }}{C^{ - 1}} \\\
So, net force acting on point charge of +1μC + 1\mu C is Given By
F=qE ⇒F=1×10−6×12727.9 ∴F=12.73×10−2N F = qE \\\ \Rightarrow F = 1 \times {10^{ - 6}} \times 12727.9 \\\ \therefore F = 12.73 \times {10^{ - 2}}N \\\
Hence, the net force acting on +1μC + 1\mu C is 12.73×10−2N12.73 \times {10^{ - 2}}N.

Note: While simplifying the forces don’t make mistakes in angles go step by step calculation to avoid mistakes. The repulsive or attractive interaction between any two charged bodies is called an electric force. Similar to any force, its impact and effects on the given body are described by Newton's laws of motion.