Question
Question: Let \(ABC\) be an equilateral triangle inscribed in a circle \(O\) . \(M\) is a point on the arc \(B...
Let ABC be an equilateral triangle inscribed in a circle O . M is a point on the arc BC . Lines AM,BM and CM are drawn. Then \mathop {AM}\limits^{\\_\\_\\_\\_\\_} is:
\left( a \right){\text{ equal to }}\mathop {BM}\limits^{\\_\\_\\_\\_\\_} + \mathop {CM}\limits^{\\_\\_\\_\\_\\_} 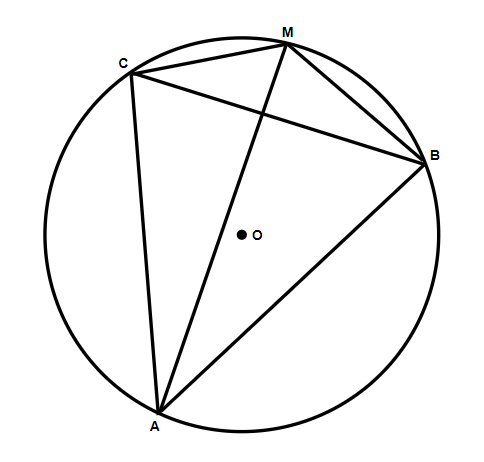
\left( b \right){\text{ less than }}\mathop {BM}\limits^{\\_\\_\\_\\_\\_} + \mathop {CM}\limits^{\\_\\_\\_\\_\\_}
\left( c \right){\text{ greater than }}\mathop {BM}\limits^{\\_\\_\\_\\_\\_} + \mathop {CM}\limits^{\\_\\_\\_\\_\\_}
\left( d \right){\text{ equal, less than, or greater than }}\mathop {BM}\limits^{\\_\\_\\_\\_\\_} + \mathop {CM}\limits^{\\_\\_\\_\\_\\_} ,{\text{ depending upon position upon M}}
Solution
For proving this type of question, all we can do is proceed with the information and figure provided. So we can see that since the O is the center which lies on AM hence, AM will be equal to 2R. And also AM is perpendicular to BC and also AD is perpendicular to the same. So by using this we will equate both of them and get the value. And on solving it we will be able to find the required equation.
Complete answer:
First of all, we will assume this is an ideal case. And since, from the information provided, we can say that O is the center which lies on AM .
Therefore, AM=2R and here R will be the radius of the circle.
Also, we can see that AM⊥BC , so from this O will be the point which lies on AM and BC .
Here, AD⊥BC , so from the figure we can write it in fraction as
⇒OBBD=23
Now let us assume AB=BC=CA=a , OA = OB = OC = R
Therefore, on substituting the values, we will get the relation as
⇒2Ra=23
And by doing the cross multiplication and solving the above equation, we get the equation as
⇒a=3R
Since, we have AM=2R ,
So by using the trigonometric properties, we have
⇒BM=CM=cos30∘BD
And on solving the above line, we get the equation as
⇒3a
So from this now we can have the sum of BM&CM
On adding the sum, we will get 32a
Now on substituting the value of a , we get the equation as
⇒32×3R
And on solving the above line we get
⇒2R=AM
Therefore, from this, we can say \mathop {AM}\limits^{\\_\\_\\_\\_\\_} = \mathop {BM}\limits^{\\_\\_\\_\\_\\_} + \mathop {CM}\limits^{\\_\\_\\_\\_\\_} .
Hence, the option (a) is correct.
Note: For solving this type of question we need to know the geometry and its properties ideas so that we can equate the equation. Also, the use of trigonometry should be known to us as they are used sometimes. So by using the relation we will expand the equation and solve it then we can easily get to the solution.
