Question

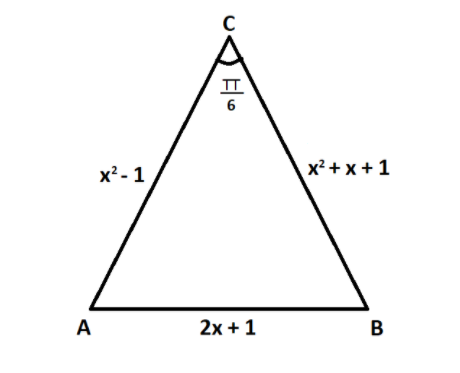
Let ABC be a triangle such that $\angle ACB = \dfrac{\pi }{6}$ and let a, b and c denote the length of the sides opposite to A, B and C respectively. The value(s) of x for which $a = {x^2} + x + 1$, $b = {x^2} - 1$ and $c = 2x + 1$ is(are)
A. $- \left( {2 + \sqrt 3 } \right)$
B. $1 + \sqrt 3$
C. $2 + \sqrt 3$
D. $4\sqrt 3$

Answer 1

To solve this question, we will use the concept of Cosine rule (the law of Cosine). According to the Cosine rule, the square of the length of any side of a triangle equals to the sum of the squares of the length of the other sides minus twice of their product multiplied by the cosine of their included angle, i.e. ${a^2} = {b^2} + {c^2} - 2bc\cos A$, ${b^2} = {a^2} + {c^2} - 2ac\cos B$ and ${c^2} = {a^2} + {b^2} - 2ab\cos C$

Complete step-by-step answer :

Given that,
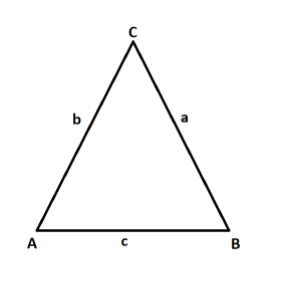
ABC is a triangle and $\angle ACB = \dfrac{\pi }{6}$
a = length of side opposite to A.
b = length of side opposite to B.
c = length of side opposite to C.
we have to find out the value of x, when $a = {x^2} + x + 1$, $b = {x^2} - 1$ and $c = 2x + 1$
So,
As we know that,
According to the Cosine rule, the square of the length of any side of a triangle equals to the sum of the squares of the length of the other sides minus twice their product multiplied by the cosine of their included angle.
We have given,
$\angle ACB = \dfrac{\pi }{6}$
Therefore, applying the Cosine rule for $\angle C$,
${c^2} = {a^2} + {b^2} - 2ab\cos C$
This can also be written as:
$\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Putting the value of a, b and c in the above equation, we will get
$\cos \dfrac{\pi }{6} = \dfrac{{{{\left( {{x^2} + x + 1} \right)}^2} + {{\left( {{x^2} - 1} \right)}^2} - {{\left( {2x + 1} \right)}^2}}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}$
By using the appropriate identities, we will solve this
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^4} + 2{x^3} - 3{x^2} - 2x + 1} \right)}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}$
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^2} + 2x - 1} \right)\left( {{x^2} - 1} \right)}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}$
Dividing $\left( {{x^2} - 1} \right)$ from numerator and denominator, we will get
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^2} + 2x - 1} \right)}}{{2\left( {{x^2} + x + 1} \right)}}$
$\Rightarrow \sqrt 3 = \dfrac{{\left( {2{x^2} + 2x - 1} \right)}}{{\left( {{x^2} + x + 1} \right)}}$
Now taking $\left( {{x^2} + x + 1} \right)$ to the left side,
$\Rightarrow \sqrt 3 \left( {{x^2} + x + 1} \right) = \left( {2{x^2} + 2x - 1} \right)$
Simplifying this,
$\Rightarrow {x^2}\left( {\sqrt 3 - 2} \right) + x\left( {\sqrt 3 - 2} \right) + \left( {\sqrt 3 + 1} \right) = 0$ ……… (i)
Now, we find out the roots of the above quadratic equation using the formula,
$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$ ……… (ii)
Comparing equation (i) with $a{x^2} + bx + c = 0$, we will get
$a = b = \sqrt 3 - 2$ and $c = \sqrt 3 + 1$
Putting these values in equation (ii),

$$\Rightarrow x = \dfrac{{ - \left( {\sqrt 3 - 2} \right) \pm \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2} - 4\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 + 1} \right)} }}{{2\left( {\sqrt 3 - 2} \right)}} \\\ \Rightarrow x = \dfrac{{ - \left( {\sqrt 3 - 2} \right) \pm \sqrt {\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 - 2 - 4\sqrt 3 - 4} \right)} }}{{2\left( {\sqrt 3 - 2} \right)}} \\\ \Rightarrow x = \dfrac{{\left( {2 - \sqrt 3 } \right) \pm \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} \\\$$

Now, we get 2 values of x,
$x = \dfrac{{\left( {2 - \sqrt 3 } \right) + \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} = \dfrac{1}{{\left( {\sqrt 3 - 2} \right)}}$,
Rationalising it,

$$x = \dfrac{1}{{\left( {\sqrt 3 - 2} \right)}} \times \dfrac{{\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)}} \\\ x = - \left( {\sqrt 3 + 2} \right) \\\$$

Or,
$x = \dfrac{{\left( {2 - \sqrt 3 } \right) - \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} = \dfrac{{\left( {1 - \sqrt 3 } \right)}}{{\left( {\sqrt 3 - 2} \right)}}$,
Rationalising it,

$$x = \dfrac{{\left( {1 - \sqrt 3 } \right)}}{{\left( {\sqrt 3 - 2} \right)}} \times \dfrac{{\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)}} \\\ x = \left( {1 + \sqrt 3 } \right) \\\$$

Hence, the value of x will be $\left( {1 + \sqrt 3 } \right)$ as x > 0.
Therefore, the correct answer is option (B).

Note : Whenever we ask such questions, we have to remember that Cosine rule will be used when two sides and included angles are given or when three sides of a triangle is given. The sine rule states that the sides of a triangle are proportional to the sines of the opposite angles, i.e. given as: $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$