Question

Let ABC and ABC’ be two non-congruent triangles with sides AB = 4, AC = AC’ = $2\sqrt{2}$ and angle B = ${{30}^{\circ }}$. The absolute value of the difference between the areas of these triangles is?

Answer 1

In this problem, we have to find the absolute value of the difference between the areas of the given triangles. We are given that ABC and ABC’ be two non-congruent triangles with sides AB = 4, AC = AC’ = $2\sqrt{2}$ and angle B = ${{30}^{\circ }}$. Here we can use the sine rule to find the angle value for C and C’. We can then use the area of the formula to find the area for both the triangles. We can then find the difference for both the areas of the triangles.

Complete step by step solution:
We know that the given triangles ABC and ABC’.
We are also given AB = 4, AC = AC’ = $2\sqrt{2}$ and angle B = ${{30}^{\circ }}$.
We can now use the sine rule for the triangle ABC.
$\Rightarrow \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$

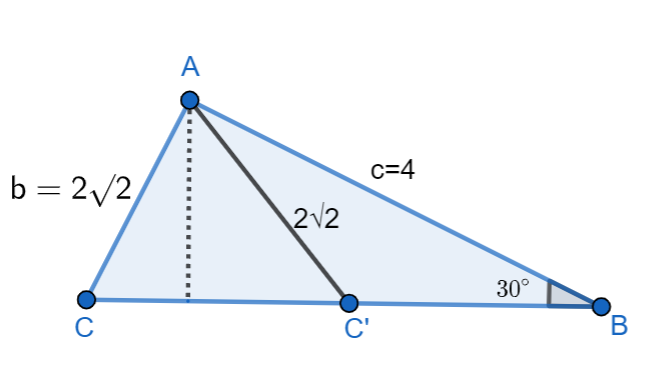
We can now substitute the given values in the sine rule, we get
$\Rightarrow \dfrac{a}{\sin A}=\dfrac{2\sqrt{2}}{\sin {{30}^{\circ }}}=\dfrac{4}{\sin C}$……. (1)
We can now find the value of angle C and C’ from the above step, we get

& \Rightarrow \sin C=\dfrac{4\sin {{30}^{\circ }}}{2\sqrt{2}}=\dfrac{4}{2\sqrt{2}\sqrt{2}}=1 \\\ & \Rightarrow C={{45}^{\circ }} \\\ \end{aligned}$$ We can see that if $$C={{45}^{\circ }}$$, then the remaining angle value will be $$C'={{135}^{\circ }}$$. We can now find the angle value of A as we know that the sum of the angles of three sides is equal to $${{180}^{\circ }}$$ . For $$C={{45}^{\circ }}$$, we get $$\Rightarrow A={{180}^{\circ }}-\left( {{45}^{\circ }}+{{30}^{\circ }} \right)={{105}^{\circ }}$$ For $$C'={{135}^{\circ }}$$, we get $$\Rightarrow A={{180}^{\circ }}-\left( {{135}^{\circ }}+{{30}^{\circ }} \right)={{15}^{\circ }}$$ We can now find the area of triangle ABC and ABC’, Area of triangle ABC $$\begin{aligned} & \Rightarrow \dfrac{1}{2}AB\times AC\sin A=\dfrac{1}{2}\times 4\times 2\sqrt{2}\sin {{105}^{\circ }} \\\ & \Rightarrow 2\left( \sqrt{3}+1 \right) \\\ \end{aligned}$$ Area of triangle ABC’ $$\begin{aligned} & \Rightarrow \dfrac{1}{2}AB\times AC\sin A=\dfrac{1}{2}\times 4\times 2\sqrt{2}\sin {{15}^{\circ }} \\\ & \Rightarrow 2\left( \sqrt{3}-1 \right) \\\ \end{aligned}$$ We can now find the difference for the given triangles, we get $$\Rightarrow 2\left( \sqrt{3}+1 \right)-2\left( \sqrt{3}-1 \right)=4$$  Therefore, the absolute value of the difference between the areas of these triangles is 4. **Note:** Students make mistakes while finding the remaining angle values using the sine rule. We should also remember that the sum of angles of three sides of a triangle is always equal to $${{180}^{\circ }}$$. We should also remember some trigonometric degree values to be used in these types of problems.