Question
Question: Let $AB: x+2y-3=0$, $BC: 2x-y+5=0$ and $AC: x-2=0$ be sides of $\triangle ABC$. Match the entries of...
Let AB:x+2y−3=0, BC:2x−y+5=0 and AC:x−2=0 be sides of △ABC. Match the entries of List-I with the correct entries of List-II.
| List-I | List-II |
|---|---|
| (P) Circumcentre of △ABC, is | (1) (−57,511) |
| (Q) Centroid of △ABC, is | (2) (513,30131) |
| (R) Orthocentre of △ABC, is | (3) (2,419) |
| (S) Vertex B, is | (4) (1,1) |
| (5) The point which divides the distance between orthocentre and circumcentre in the ratio 2:1 internally |
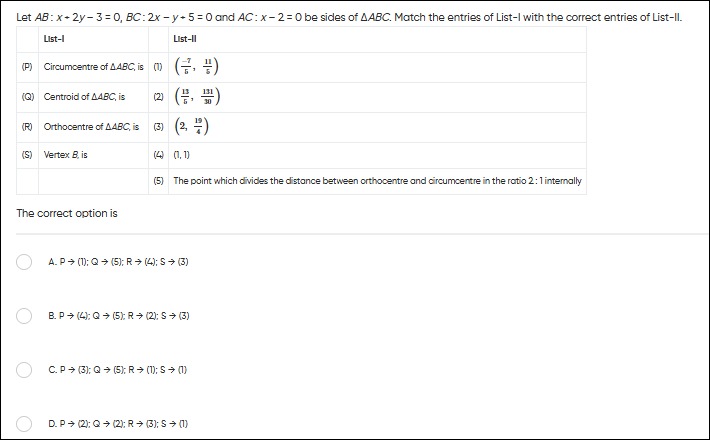
P→(1); Q→(5); R→(4); S→(3)
P→(4); Q→(5); R→(2); S→(3)
P→(3); Q→(5); R→(1); S→(1)
P→(2); Q→(2); R→(3); S→(1)
P→(3); Q→(5); R→(1); S→(1)
Solution
The vertices are A(2, 1/2), B(-7/5, 11/5), and C(2, 9). Since mAB=−1/2 and mBC=2, AB is perpendicular to BC. Thus, △ABC is right-angled at B. Orthocentre (R) is the vertex B: (−7/5,11/5), which matches (1). Circumcentre (P) is the midpoint of hypotenuse AC: ((2+2)/2,(1/2+9)/2)=(2,19/4), which matches (3). Centroid (Q) is the point dividing the segment joining orthocentre and circumcentre in the ratio 2:1 internally. This is the definition given in (5). Vertex B (S) is (−7/5,11/5), which matches (1). Thus, P→(3); Q→(5); R→(1); S→(1).
