Question
Question: Let $a_n=1-\frac{2n^2}{1+\sqrt{1+4n^4}}, n=1,2,3,...$ Then the value of $\sqrt{a_1}+2\sqrt{a_2}+....
Let
an=1−1+1+4n42n2,n=1,2,3,...
Then the value of
a1+2a2+...+20a20
is ?
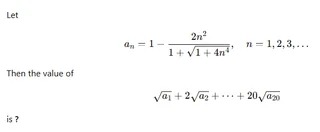
14
Solution
The problem asks for the sum of a series involving an. First, we need to simplify the expression for an.
The given expression for an is: an=1−1+1+4n42n2
To simplify, we can rationalize the denominator of the fraction 1+1+4n42n2. Multiply the numerator and denominator by the conjugate of the denominator, which is (1−1+4n4): 1+1+4n42n2=1+1+4n42n2×1−1+4n41−1+4n4 =12−(1+4n4)22n2(1−1+4n4) =1−(1+4n4)2n2(1−1+4n4) =−4n42n2(1−1+4n4) =−2n21−1+4n4 =2n21+4n4−1
Now, substitute this back into the expression for an: an=1−(2n21+4n4−1) an=2n22n2−(1+4n4−1) an=2n22n2−1+4n4+1
Next, we need to find an. Let's simplify the numerator: 2n2+1−1+4n4. We use the denesting formula for square roots: X±Y=2X+X2−Y±2X−X2−Y. Here, X=2n2+1 and Y=1+4n4. Calculate X2−Y: X2−Y=(2n2+1)2−(1+4n4) X2−Y=(4n4+4n2+1)−(1+4n4) X2−Y=4n2 So, X2−Y=4n2=2n (since n is a positive integer, 2n>0).
Now, apply the denesting formula to the numerator 2n2+1−1+4n4: 2n2+1−1+4n4=2(2n2+1)+2n−2(2n2+1)−2n =22n2+2n+1−22n2−2n+1
So, an becomes: an=2n222n2+2n+1−22n2−2n+1 an=n222n2+2n+1−22n2−2n+1 an=2n2n2+2n+1−2n2−2n+1
This is the simplified form of an. Now we need to evaluate the sum S=a1+2a2+...+20a20. The general term in the sum is kak. So, kak=k(2k2k2+2k+1−2k2−2k+1) kak=21(2k2+2k+1−2k2−2k+1)
Let f(k)=2k2−2k+1. Then f(k+1)=2(k+1)2−2(k+1)+1=2(k2+2k+1)−2k−2+1=2k2+4k+2−2k−2+1=2k2+2k+1. So, the term kak can be written as: kak=21(f(k+1)−f(k))
This is a telescoping sum. Let's write out the terms: For k=1: 1a1=21(f(2)−f(1)) For k=2: 2a2=21(f(3)−f(2)) For k=3: 3a3=21(f(4)−f(3)) ... For k=20: 20a20=21(f(21)−f(20))
Summing these terms: S=∑k=120kak=21∑k=120(f(k+1)−f(k)) S=21[(f(2)−f(1))+(f(3)−f(2))+...+(f(21)−f(20))] S=21[f(21)−f(1)]
Now, we need to calculate f(1) and f(21). f(k)=2k2−2k+1. For k=1: f(1)=2(1)2−2(1)+1=2−2+1=1=1. For k=21: f(21)=2(21)2−2(21)+1=2(441)−42+1=882−42+1=841. We know that 202=400, 302=900. The last digit is 1, so it could be 212 or 292. 292=(30−1)2=900−60+1=841. So, f(21)=29.
Substitute these values back into the sum S: S=21[29−1] S=21[28] S=14
The value of the given sum is 14.
