Question

Let $A_n, (n \in N)$ be a matrix of order $(2n-1) \times (2n-1)$, such that $a_{ij} = 0 \forall i \neq j$ and $a_{ij} = n^2 + i + 1 - 2n \forall i = j$ where $a_{ij}$ denotes the element of $i^{th}$ row and $j^{th}$ column of $A_n$. Let $T_n = (-1)^n \times$(sum of all the elements of $A_n$). Find the value of $\left[\frac{\sum_{n=1}^{102} T_n}{520200}\right]$, (greatest integer function).

Answer 1

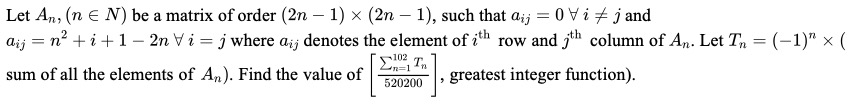
2

Answer 2

The matrix $A_n$ is of order $(2n-1) \times (2n-1)$. The elements are given by $a_{ij} = 0$ for $i \neq j$ and $a_{ij} = n^2 + i + 1 - 2n$ for $i = j$. This means $A_n$ is a diagonal matrix. The diagonal elements are $d_i = a_{ii} = n^2 + i + 1 - 2n$ for $i = 1, 2, \dots, 2n-1$.

The sum of all elements of $A_n$ is the sum of its diagonal elements: $S_n = \sum_{i=1}^{2n-1} (n^2 + i + 1 - 2n)$ $S_n = \sum_{i=1}^{2n-1} (n^2 - 2n + 1) + \sum_{i=1}^{2n-1} i$ $S_n = (2n-1)(n^2 - 2n + 1) + \frac{(2n-1)(2n-1+1)}{2}$ $S_n = (2n-1)(n-1)^2 + \frac{(2n-1)(2n)}{2}$ $S_n = (2n-1)(n-1)^2 + (2n-1)n$ $S_n = (2n-1)((n-1)^2 + n)$ $S_n = (2n-1)(n^2 - 2n + 1 + n)$ $S_n = (2n-1)(n^2 - n + 1)$.

We observe that $n^2 - n + 1$ is a factor in the sum of cubes identity $a^3 + b^3 = (a+b)(a^2 - ab + b^2)$. Let $a=n$ and $b=1$. Then $n^3 + 1^3 = (n+1)(n^2 - n + 1)$. Let's try to express $S_n$ in terms of cubes. Consider $n^3 + (n-1)^3 = n^3 + (n^3 - 3n^2 + 3n - 1) = 2n^3 - 3n^2 + 3n - 1$. Let's expand $S_n = (2n-1)(n^2 - n + 1) = 2n(n^2 - n + 1) - 1(n^2 - n + 1) = 2n^3 - 2n^2 + 2n - n^2 + n - 1 = 2n^3 - 3n^2 + 3n - 1$. Thus, $S_n = n^3 + (n-1)^3$.

$T_n = (-1)^n \times S_n = (-1)^n (n^3 + (n-1)^3)$.

We need to calculate $\sum_{n=1}^{102} T_n = \sum_{n=1}^{102} (-1)^n (n^3 + (n-1)^3)$. Let's write out the terms: $T_1 = (-1)^1 (1^3 + (1-1)^3) = - (1^3 + 0^3)$ $T_2 = (-1)^2 (2^3 + (2-1)^3) = + (2^3 + 1^3)$ $T_3 = (-1)^3 (3^3 + (3-1)^3) = - (3^3 + 2^3)$ $T_4 = (-1)^4 (4^3 + (4-1)^3) = + (4^3 + 3^3)$ ... $T_{101} = (-1)^{101} (101^3 + (101-1)^3) = - (101^3 + 100^3)$ $T_{102} = (-1)^{102} (102^3 + (102-1)^3) = + (102^3 + 101^3)$

The sum is $\sum_{n=1}^{102} T_n = -(1^3 + 0^3) + (2^3 + 1^3) - (3^3 + 2^3) + (4^3 + 3^3) - \dots - (101^3 + 100^3) + (102^3 + 101^3)$.

Grouping terms in pairs: $T_1+T_2 = -(1^3+0^3) + (2^3+1^3) = 2^3 - 0^3 = 2^3$. $T_3+T_4 = -(3^3+2^3) + (4^3+3^3) = 4^3 - 2^3$. $T_5+T_6 = -(5^3+4^3) + (6^3+5^3) = 6^3 - 4^3$. ... $T_{2k-1}+T_{2k} = -( (2k-1)^3 + (2k-2)^3 ) + ( (2k)^3 + (2k-1)^3 ) = (2k)^3 - (2k-2)^3$. The sum $\sum_{n=1}^{102} T_n$ has 102 terms, which can be grouped into 51 pairs. $\sum_{n=1}^{102} T_n = \sum_{k=1}^{51} (T_{2k-1} + T_{2k}) = \sum_{k=1}^{51} ((2k)^3 - (2k-2)^3)$. Let $m=2k$. The sum becomes $\sum_{k=1}^{51} (m^3 - (m-2)^3)$ where $m$ takes values $2, 4, 6, \dots, 102$. This is a telescoping sum: $k=1: (2^3 - 0^3)$ $k=2: (4^3 - 2^3)$ $k=3: (6^3 - 4^3)$ ... $k=51: (102^3 - 100^3)$ Summing these terms: $(2^3 - 0^3) + (4^3 - 2^3) + (6^3 - 4^3) + \dots + (102^3 - 100^3)$ $= -0^3 + (2^3 - 2^3) + (4^3 - 4^3) + \dots + (100^3 - 100^3) + 102^3$ $= 102^3$.

So, $\sum_{n=1}^{102} T_n = 102^3$. We need to calculate the value of $\left[\frac{102^3}{520200}\right]$. $102^3 = 102 \times 102 \times 102$. $102^2 = (100+2)^2 = 10000 + 400 + 4 = 10404$. $102^3 = 10404 \times 102 = 10404 \times (100+2) = 1040400 + 10404 \times 2 = 1040400 + 20808 = 1061208$.

The required value is $\left[\frac{1061208}{520200}\right]$. Let's perform the division: $1061208 = 2 \times 520200 + 20808$. $\frac{1061208}{520200} = 2 + \frac{20808}{520200}$. Since $0 < \frac{20808}{520200} < 1$, the greatest integer is 2.

The value of $\left[\frac{\sum_{n=1}^{102} T_n}{520200}\right]$ is 2.

Subject: Mathematics Chapter: Matrices Topic: Types of Matrices (Diagonal Matrix), Summation of Series, Greatest Integer Function

Difficulty level: Medium (Requires understanding of matrix properties, summation techniques, and recognizing patterns for telescoping sums)

Question type: Integer