Question
Question: Let $a_k = \frac{k}{(k-1)^{4/3} + k^{4/3} + (k+1)^{4/3}}$ and $S_n = \sum_{k=1}^{n} a_k$, then...
Let ak=(k−1)4/3+k4/3+(k+1)4/3k and Sn=∑k=1nak, then
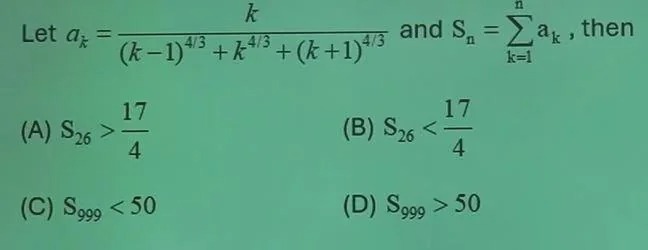
S26>417
S26<417
S999<50
S999>50
Options (B) and (C)
Solution
We wish to study
ak=(k−1)4/3+k4/3+(k+1)4/3kand then
Sn=k=1∑nak.A key observation is that for large k the dominant behavior is given by the powers of k. Notice that
(k−1)4/3∼k4/3,k4/3∼k4/3,(k+1)4/3∼k4/3.In fact, the denominator behaves approximately as
(k−1)4/3+k4/3+(k+1)4/3≈3k4/3for large k.Thus for large k we have
ak≈3k4/3k=3k1/31.Once you have the asymptotic approximation
Sn≈k=1∑n3k1/31,it is natural to use an integral to estimate the sum. In particular,
k=1∑n3k1/31≈31∫1nx−1/3dx.Since
∫x−1/3dx=23x2/3+C,we get
Sn≈31⋅23(n2/3−1)=2n2/3−1.Now let’s apply this to the two cases:
- For n=26:
We estimate
S26≈2262/3−1.Since 271/3=3 and 261/3 is slightly less (approximately 2.96), we have
262/3≈(2.96)2≈8.77.Then,
S26≈28.77−1=27.77≈3.885.Now, 417=4.25. Thus S26≈3.89<4.25. Therefore option (B) is true.
- For n=999:
Similarly,
S999≈29992/3−1.Note that 10001/3=10 so 9991/3 is very nearly 10 and hence 9992/3 is nearly 102=100. In fact, one may estimate
S999≈2100−1=299=49.5.This shows that S999<50 so option (C) is true.
Thus our conclusions are:
- (B) S26<417
- (C) S999<50
Minimal Core Explanation
- Asymptotic behavior: For large k, approximate ak∼3k1/31.
- Integral estimate: Sn≈31∫1nx−1/3dx=2n2/3−1.
- Apply for n=26: 2262/3−1≈3.89<4.25=417.
- Apply for n=999: 29992/3−1≈49.5<50.
