Question
Question: Let $a_1, a_2, a_3, ...$ be in an A.P. such that $\sum_{k=1}^{12} a_{2k-1} = -\frac{72}{5} a_1, a_1 ...
Let a1,a2,a3,... be in an A.P. such that ∑k=112a2k−1=−572a1,a1=0. If ∑k=1nak=0, then n is:
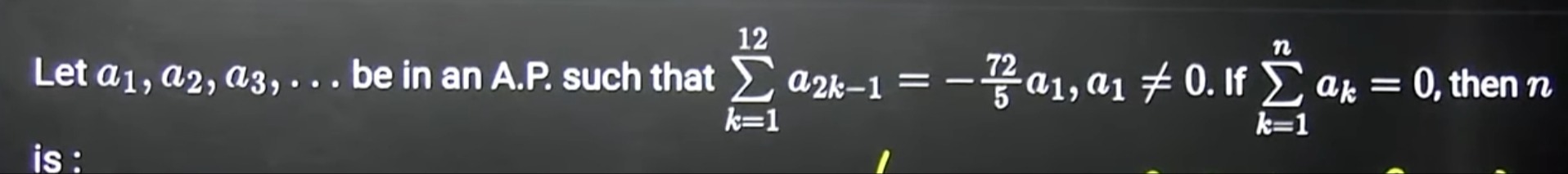
11
Solution
Let the arithmetic progression (AP) be denoted by a1,a2,a3,… with the first term a1 and common difference d.
The terms a2k−1 for k=1,2,…,12 are a1,a3,a5,…,a23. This sequence of terms is itself an AP with the first term A=a1 and a common difference D=a3−a1=(a1+2d)−a1=2d. There are N=12 terms in this sum.
The sum of these terms is given by the formula for the sum of an AP: SN=2N[2A+(N−1)D] ∑k=112a2k−1=212[2a1+(12−1)(2d)] =6[2a1+11(2d)] =6[2a1+22d] =12a1+132d.
We are given that ∑k=112a2k−1=−572a1. Therefore, 12a1+132d=−572a1.
Rearranging the terms to find a relationship between a1 and d: 132d=−572a1−12a1 132d=(−572−560)a1 132d=−5132a1.
Since a1=0, we can divide by 132a1: d=−51a1. This implies a1=−5d. Since a1=0, it follows that d=0.
The second condition is ∑k=1nak=0. This is the sum of the first n terms of the AP, Sn. The formula for Sn is: Sn=2n[2a1+(n−1)d].
We are given Sn=0. 2n[2a1+(n−1)d]=0. Since n represents the number of terms, n must be a positive integer, so n=0. Thus, we must have: 2a1+(n−1)d=0.
Substitute the relation a1=−5d into this equation: 2(−5d)+(n−1)d=0 −10d+(n−1)d=0.
Factor out d: d(−10+n−1)=0 d(n−11)=0.
Since we established that d=0 (because a1=0), we can conclude that: n−11=0 n=11.
