Question
Question: Let $a_1, a_2, a_3, ...$ be an A.P. If $\sum_{r=1}^{\infty} \frac{a_r}{2^r} = 4$, then $4a_2$ is equ...
Let a1,a2,a3,... be an A.P. If ∑r=1∞2rar=4, then 4a2 is equal to _____.
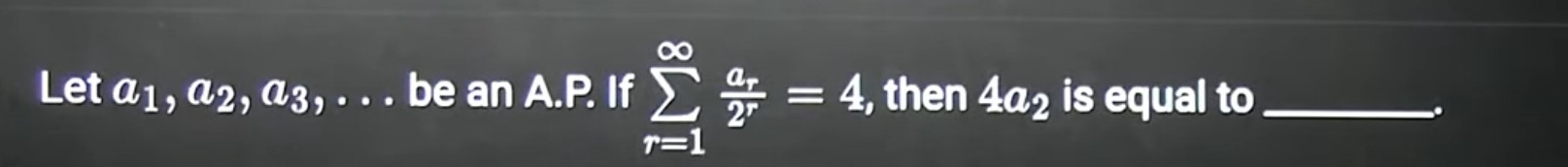
16
Solution
Let the arithmetic progression be denoted by ar=a+(r−1)d, where a=a1 is the first term and d is the common difference. We are given the sum of an infinite series: ∑r=1∞2rar=4 Substituting the expression for ar: ∑r=1∞2ra+(r−1)d=4 We can split this sum into two parts: ∑r=1∞2ra+∑r=1∞2r(r−1)d=4 a∑r=1∞(21)r+d∑r=1∞2rr−1=4 The first part is a geometric series with first term 1/2 and common ratio 1/2. The sum is: ∑r=1∞(21)r=1−2121=2121=1 So, the first term of the equation becomes a×1=a.
The second part is d∑r=1∞2rr−1. Let's evaluate the sum T=∑r=1∞2rr−1: T=211−1+222−1+233−1+244−1+… T=20+41+82+163+… T=41+82+163+… This is an arithmetico-geometric series. Multiply T by the common ratio 1/2: 21T=81+162+323+… Subtracting 21T from T: T−21T=(41+82+163+…)−(81+162+323+…) 21T=41+(82−81)+(163−162)+(324−323)+… 21T=41+81+161+321+… This is a geometric series with first term 1/4 and common ratio 1/2. 21T=1−2141=2141=21 So, T=1.
Substituting the sums back into the equation: a(1)+d(1)=4 a+d=4 The second term of the AP is a2=a+(2−1)d=a+d. Therefore, a2=4.
The question asks for the value of 4a2. 4a2=4×4=16
Alternatively, using the formula for the sum of an arithmetico-geometric series ∑n=1∞[A+(n−1)D]xn−1=1−xA+(1−x)2Dx for ∣x∣<1. The given sum is S=∑r=1∞2ra+(r−1)d=21∑r=1∞[a+(r−1)d](21)r−1. Here, A=a, D=d, and x=1/2. The sum inside the bracket is 1−1/2a+(1−1/2)2d(1/2)=1/2a+(1/2)2d/2=2a+1/4d/2=2a+2d. So, S=21(2a+2d)=a+d. Given S=4, so a+d=4. Since a2=a+d, we have a2=4. Thus, 4a2=4×4=16.
The sum of the given arithmetico-geometric series ∑r=1∞2rar where ar is an AP, evaluates to a1+d, where a1 is the first term and d is the common difference of the AP. Given this sum is 4, we have a1+d=4. The second term of the AP is a2=a1+d. Therefore, a2=4. The value of 4a2 is 4×4=16.
