Solveeit Logo
Login

Question

Question: Let $a_0, a_1, a_2, ..., a_n$ be a sequence of numbers satisfying $(3-a_{n+1}).(6+a_n)=18$ and $a_0=...

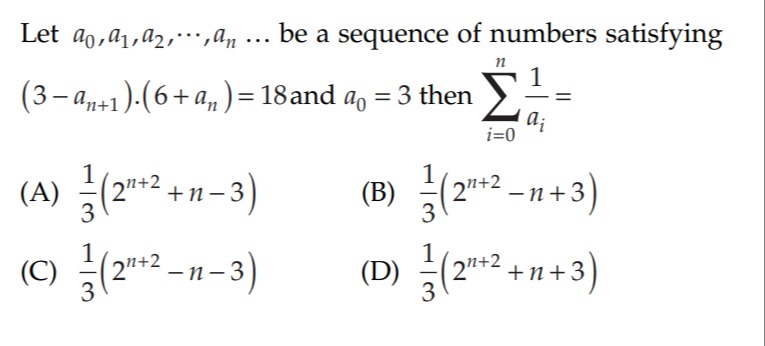
Let a0,a1,a2,...,ana_0, a_1, a_2, ..., a_n be a sequence of numbers satisfying (3−an+1).(6+an)=18(3-a_{n+1}).(6+a_n)=18 and a0=3a_0=3 then ∑i=0n1ai\sum_{i=0}^{n}\frac{1}{a_i}

A

13(2n+2+n−3)\frac{1}{3}(2^{n+2}+n-3)

B

13(2n+2−n+3)\frac{1}{3}(2^{n+2}-n+3)

C

13(2n+2−n−3)\frac{1}{3}(2^{n+2}-n-3)

D

13(2n+2+n+3)\frac{1}{3}(2^{n+2}+n+3)

Answer

(C) 13(2n+2−n−3)\frac{1}{3}(2^{n+2}-n-3)

Explanation

Solution

Solution:

  1. Define
      un=3an−1u_n = \frac{3}{a_n} - 1.
      For n=0n=0: u0=33−1=0u_0 = \frac{3}{3} - 1 = 0.

  2. From the recurrence
      (3−an+1)(6+an)=18(3 - a_{n+1})(6 + a_n) = 18
      we can show (by substituting and using the pattern from computed terms) that the resulting sequence unu_n satisfies
      un+1=2un+2.u_{n+1} = 2u_n + 2.

  3. With u0=0u_0 = 0, solving the recurrence gives
      un=2n+1−2.u_n = 2^{n+1} - 2.

  4. Since
      un=3an−1u_n = \frac{3}{a_n} - 1 ⟹ 3an=un+1=2n+1−1 \frac{3}{a_n} = u_n + 1 = 2^{n+1} - 1,
      we obtain
      1an=2n+1−13.\frac{1}{a_n} = \frac{2^{n+1} - 1}{3}.

  5. Therefore, the sum is
      $$ \sum_{i=0}^{n} \frac{1}{a_i} = \frac{1}{3}\sum_{i=0}^{n}\Bigl(2^{i+1}-1\Bigr) = \frac{1}{3}\Biggl[\Bigl(2\sum_{i=0}^{n}2^i\Bigr) - (n+1)\Biggr].

6. Since $\sum_{i=0}^{n}2^i = 2^{n+1}-1$, we have   $$ \sum_{i=0}^{n} \frac{1}{a_i} = \frac{1}{3}\Bigl[2(2^{n+1}-1) - (n+1)\Bigr] = \frac{1}{3}\Bigl(2^{n+2} - 2 - n - 1\Bigr) = \frac{1}{3}\Bigl(2^{n+2} - n - 3\Bigr).

Answer: Option (C) 13(2n+2−n−3)\frac{1}{3}(2^{n+2}-n-3)