Question

Let $A = \{x \mid x^3 + x^2 - px + q = 0, p, q, \in R\}$ and $B = \{x \mid x^2 - qx + 2 = 0, q \in R\}$ be the sets. If $n(A \cap B) = 2$ and $x_0 \in (A - B)$, then find the value of $|p - q + x_0|$.

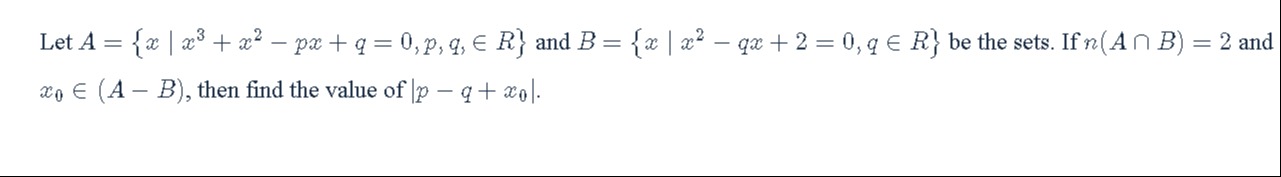
Answer 1

3

Answer 2

Let the two common roots (since n(A ∩ B) = 2) be $\alpha$ and $\beta$, which are the roots of the quadratic

$$x^2 - qx + 2 = 0.$$

Then:

$$\alpha + \beta = q,\quad \alpha\beta = 2.$$

The cubic equation

$$x^3 + x^2 - px + q = 0$$

has roots $\alpha$, $\beta$, and $\gamma$ (with $x_0 = \gamma \notin B$). Expressing the cubic as

$$(x-\alpha)(x-\beta)(x-\gamma) = x^3 - (\alpha+\beta+\gamma)x^2 + (\alpha\beta + \alpha\gamma + \beta\gamma)x - \alpha\beta\gamma,$$

comparing coefficients we obtain:

1. Coefficient of $x^2$:

$$-(\alpha+\beta+\gamma) = 1 \quad \Rightarrow \quad \alpha+\beta+\gamma = -1.$$

Thus,

$$\gamma = -1 - (\alpha+\beta) = -1 - q.$$

2. Constant term:

$$-\alpha\beta\gamma = q \quad \Rightarrow \quad \alpha\beta\gamma = -q.$$

Since $\alpha\beta = 2$, we have:

$$2\gamma = -q \quad \Rightarrow \quad \gamma = -\frac{q}{2}.$$

Equate the two expressions for $\gamma$:

$$-1 - q = -\frac{q}{2}.$$

Multiplying by 2:

$$-2 - 2q = -q \quad \Rightarrow \quad -2q + q = 2 \quad \Rightarrow \quad -q = 2 \quad \Rightarrow \quad q = -2.$$

Now, substitute $q = -2$ into $\gamma = -1 - q$:

$$\gamma = -1 - (-2) = 1.$$

Since $x_0 \in A - B$, we have $x_0 = \gamma = 1$.

Now, using the expression $|p - q + x_0|$:

• Find $p$ using the coefficient of $x$. The sum of the products of the roots two at a time is: $$\alpha\beta + \alpha\gamma + \beta\gamma = -p.$$ Substitute known values: $$\alpha\beta = 2 \quad \text{and} \quad \alpha + \beta = q = -2, \quad \gamma = 1,$$ so, $$2 + 1 \cdot (\alpha+\beta) = 2 + (-2) = 0 \quad \Rightarrow \quad -p = 0 \quad \Rightarrow \quad p = 0.$$

Finally, compute:

$$|p - q + x_0| = |0 - (-2) + 1| = |2 + 1| = 3.$$