Solveeit Logo
Login

Question

Question: Let a vertical tower AB have its and A on the level ground. Let C be the midpoint of AB and P be a p...

Let a vertical tower AB have its and A on the level ground. Let C be the midpoint of AB and P be a point on the ground such that AP=2ABAP = 2ABof ∠BPC=B,\angle BPC = B, then tan⁡β\tan \beta is equal to
A. 14\dfrac{1}{4}
B. 29\dfrac{2}{9}
C. 49\dfrac{4}{9}
D. 67\dfrac{6}{7}

Explanation

Solution

Draw the figure to get a clarity of the question. The term vertical means straight that it is a straight tower which has its end in the level ground. Again, level ground is nothing but a flat surface. Naming the diagram or figure helps out a lot in solving the question. So, name the figure properly and exactly according to the given condition. tan⁡β\tan \beta is the angle at the point C and point P and tan⁡β\tan \beta is nothing but perpendicularly divided by base.

Complete step by step solution:
Given:∠BPC=β\angle BPC = \beta

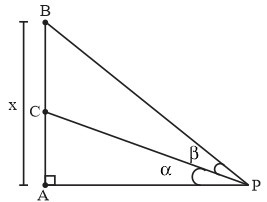
Let AB=x,AB = x,
Then AP=2AB=2xAP = 2AB = 2x
Now,
Triangle ABP is right angled triangle with BP as hypotenuse
Now, by Pythagoras theorem,

BP2=AP2+AB2 BP2=(2x)2+x2 BP2=5x2  B{P^2} = A{P^2} + A{B^2} \\\ B{P^2} = {\left( {2x} \right)^2} + {x^2} \\\ B{P^2} = 5{x^2} \\\

Therefore,
BP=5  xBP = \sqrt 5 \,\,x
Now, according to question we are told that C is mid-point of AB therefore
AC=12ABAC = \dfrac{1}{2}AB
Thus AC=x2AC = \dfrac{x}{2}
Now,
tan⁡α=(x2)(2x)=14\tan \alpha = \dfrac{{\left( {\dfrac{x}{2}} \right)}}{{\left( {2x} \right)}} = \dfrac{1}{4}
thustan⁡α=14\tan \alpha = \dfrac{1}{4}
Now, we know from figure that in triangle APB,
tan⁡(α+β)=x2x=12\tan \left( {\alpha + \beta } \right) = \dfrac{x}{{2x}} = \dfrac{1}{2}
Therefore,

tan⁡α+tan⁡β1−tan⁡α×tan⁡β=12 ⇒2(tan⁡α+tan⁡β)=1−tan⁡αtan⁡β ⇒2(14+tan⁡β)=1−14tan⁡β ⇒94tan⁡β=12 ⇒tan⁡β=29  \dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \times \tan \beta }} = \dfrac{1}{2} \\\ \Rightarrow 2\left( {\tan \alpha + \tan \beta } \right) = 1 - \tan \alpha \tan \beta \\\ \Rightarrow 2\left( {\dfrac{1}{4} + \tan \beta } \right) = 1 - \dfrac{1}{4}\tan \beta \\\ \Rightarrow \dfrac{9}{4}\tan \beta = \dfrac{1}{2} \\\ \Rightarrow \tan \beta = \dfrac{2}{9} \\\

Thus, the angle made by triangle CPB is nothing tan⁡β\tan \beta and is equal to 29\dfrac{2}{9}.
Hence the correct option is (2).
Note: In this type of question students often makes mistake while determining angle β\beta as they always choose the wrong side as thus this is the reason why it is highly recommended to draw the diagram, also remember the standard formula, as tan⁡(α+β)\tan \left( {\alpha + \beta } \right) is not tan⁡α+tan⁡β\tan \alpha + \tan \beta this is incorrect, use the correct formula to get the correct answer.