Question

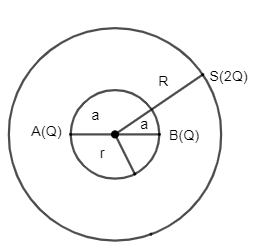
Let a total charge 2Q be distributed in a sphere of radius R, with the charge density given by p(r) = kr, where r is the distance from the centre two charges A and B of –Q each are placed on diametrically opposite points, at equal distance a form the center. If A and B do not experience force, then:
$\begin{aligned} & A.\text{ }a=\dfrac{3R}{{{2}^{\dfrac{1}{4}}}} \\\ & B.\text{ }a=\dfrac{R}{\sqrt{3}} \\\ & C.\text{ }a={{8}^{-\dfrac{1}{4}}}R \\\ & D.\text{ }a={{2}^{-\dfrac{1}{4}}}R \\\ \end{aligned}$

Answer 1

In order to find solution of this question force on A due to B must be equal to force on A due to sphere S to do so we have to find electric field on AB in order to do it we have to draw gauss’s surface inside a sphere S with radius r.
Formula used: $\oint{\overrightarrow{E}}.d\overrightarrow{A}=\dfrac{{{Q}_{in}}}{{{\varepsilon }_{0}}}$
$F=\dfrac{k{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$

Complete answer:
In order to find a solution and equilibrium condition force on A due to B is equal to force on A due to S since A and B are at equal distance and have equal charge Q.
${{F}_{AB}}={{F}_{AS}}......\left( 1 \right)$
Now force on A due to B
${{F}_{AB}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{\left( 2a \right)}^{2}}}.....\left( 2 \right)$
${{F}_{AB}}$ = electric force between A and B
k $=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$= proportionality constant
Q = charge
a = radius or distance between two charges.

Force due to S and A
${{F}_{AS}}=E.Q.....\left( 3 \right)$
First we have to find electric field E we will take gauss’s surface to find electric field on A and B now,
$\oint{\overrightarrow{E}}.d\overrightarrow{A}=\dfrac{{{Q}_{in}}}{{{\varepsilon }_{0}}}$
$\overrightarrow{E}=$ Electric field
$dA$ = area
${{Q}_{in}}=$ Charge inside a sphere
${{\varepsilon }_{0}}$ = permittivity
Electric field is constant hence
$E\oint{dA=}{}_{0}\int{^{r}}\dfrac{\rho dv}{{{\varepsilon }_{0}}}$
Now we know that area of the radius r circle is
$A=4\pi {{r}^{2}}$
And it is given in question that $\rho =kr$
Now
$\begin{aligned} & \Rightarrow E.4\pi {{r}^{2}}={}_{0}\int{^{r}}kr\dfrac{4\pi {{r}^{2}}}{{{\varepsilon }_{0}}}dr \\\ & \Rightarrow E.4\pi {{r}^{2}}=\dfrac{4\pi k}{{{\varepsilon }_{0}}}\left( \dfrac{{{r}^{4}}}{4} \right) \\\ & \therefore E=\dfrac{k{{r}^{2}}}{4{{\varepsilon }_{0}}}....\left( 4 \right) \\\ \end{aligned}$
Now we have to find k in order to do it we will use the below equation
Charge on whole sphere
$\begin{aligned} & \Rightarrow {}_{o}\int{^{2Q}}dQ={}_{o}\int{^{R}}\rho dv \\\ & \Rightarrow 2Q{{=}_{o}}\int{^{R}}kr4\pi {{r}^{2}}dr \\\ & \Rightarrow 2Q=k4\pi \dfrac{{{R}^{4}}}{4} \\\ & \therefore k=\dfrac{2Q}{\pi {{R}^{4}}} \\\ \end{aligned}$
Now substitute the value of k in equation (4)
$E=\dfrac{Q{{r}^{2}}}{2\pi {{\varepsilon }_{0}}{{R}^{4}}}$
From figure we can put r = a
$E=\dfrac{Q{{a}^{2}}}{2\pi {{\varepsilon }_{0}}{{R}^{4}}}...\left( 5 \right)$
Now put all the values in equation (1)
$\begin{aligned} & \Rightarrow {{F}_{AB}}={{F}_{AS}} \\\ & \Rightarrow \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{\left( 2a \right)}^{2}}}=E.Q \\\ \end{aligned}$
$\Rightarrow \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}^{2}}}{{{\left( 4a \right)}^{2}}}=\dfrac{Q.{{a}^{2}}}{2\pi {{\varepsilon }_{0}}{{R}^{4}}}\times Q$
$\begin{aligned} & \Rightarrow \dfrac{1}{16{{a}^{2}}}=\dfrac{{{a}^{2}}}{2{{R}^{4}}} \\\ & \Rightarrow {{a}^{4}}=\dfrac{2}{16}{{R}^{4}} \\\ & \Rightarrow {{a}^{4}}=\dfrac{1}{8}{{R}^{4}} \\\ & \therefore a={{8}^{-\dfrac{1}{4}}}R \\\ \end{aligned}$

Hence the correct option is (c).

Note:
In this question we have to consider both the charge A and B inside the sphere if we consider them outside the sphere the solution could lead us to the wrong answer or solution.