Question

Let a square matrix A of order 3 be the zero of the polynomial f (x) = x³ - 5x² + 7x - 6. If l = Tr(A) and m = det. (A) then (l + m) equals

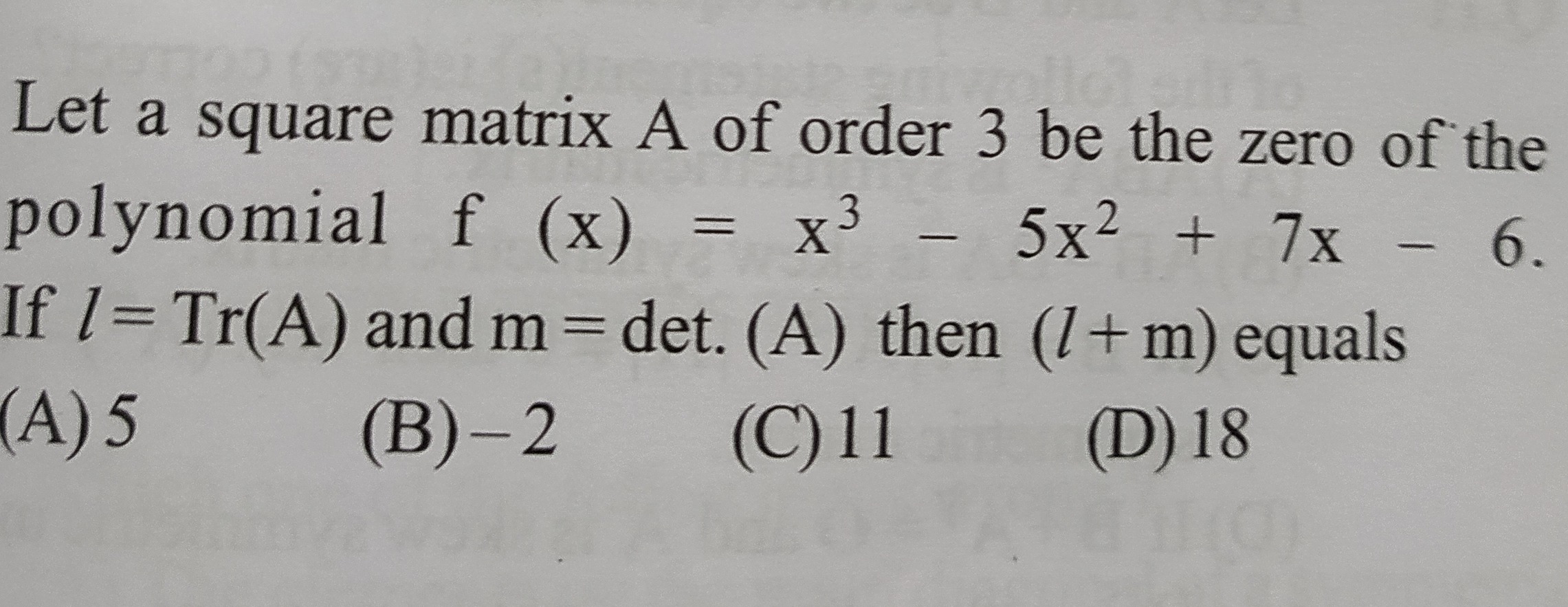
• A. 5
• B. -2
• C. 11
• D. 18

Answer 1

Answer: (C)

11

Answer 2

The matrix A satisfies the equation $A^3 - 5A^2 + 7A - 6I = 0$. By the Cayley-Hamilton theorem, a matrix satisfies its characteristic equation. For a 3x3 matrix A, the characteristic equation is $\lambda^3 - \text{Tr}(A)\lambda^2 + (\text{sum of principal minors of order 2})\lambda - \det(A) = 0$. Comparing the given polynomial equation satisfied by A with the Cayley-Hamilton equation, we identify the coefficients. The coefficient of $A^2$ gives $-\text{Tr}(A) = -5$, so $\text{Tr}(A) = 5$. The constant term gives $-\det(A)I = -6I$, so $\det(A) = 6$. Given $l = \text{Tr}(A)$ and $m = \det(A)$, we have $l=5$ and $m=6$. Therefore, $l+m = 5+6=11$.