Question

Let a plane $P$ contain two lines $\vec{r}=\hat{i}+\lambda(\hat{i}+\hat{j}), \lambda \in R$ and $\vec{r}=-\hat{i}+\mu(\hat{i}-\hat{j}), \mu \in R$. If $Q(\alpha, \beta, \lambda)$ is the foot of the perpendicular drawn from the point $M(1,0,1)$ to $P$, then $3(\alpha+\beta+\lambda)$ equals ______.

Answer 1

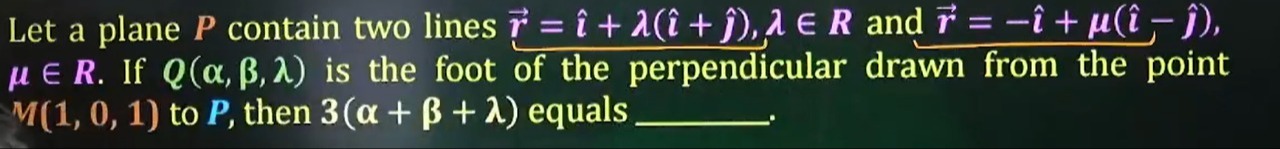
3

Answer 2

Let the first line be $L_1: \vec{r}=\hat{i}+\lambda(\hat{i}+\hat{j})$. This line passes through the point $A(1,0,0)$ and is parallel to the vector $\vec{v}_1 = \hat{i}+\hat{j}$. Let the second line be $L_2: \vec{r}=-\hat{i}+\mu(\hat{i}-\hat{j})$. This line passes through the point $B(-1,0,0)$ and is parallel to the vector $\vec{v}_2 = \hat{i}-\hat{j}$.

Since both lines lie in the plane $P$, the plane $P$ is parallel to the direction vectors $\vec{v}_1$ and $\vec{v}_2$. A normal vector to the plane $P$ is given by the cross product of $\vec{v}_1$ and $\vec{v}_2$: $\vec{n} = \vec{v}_1 \times \vec{v}_2 = (\hat{i}+\hat{j}) \times (\hat{i}-\hat{j})$ $\vec{n} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & 0 \\ 1 & -1 & 0 \end{vmatrix} = \hat{i}(0-0) - \hat{j}(0-0) + \hat{k}(-1-1) = -2\hat{k}$. We can take the normal vector $\vec{n} = \hat{k}$.

The plane $P$ contains the point $A(1,0,0)$ (or any point from either line, e.g., the intersection point $(0,-1,0)$). The equation of the plane $P$ passing through $A(1,0,0)$ with normal vector $\hat{k}$ is: $0(x-1) + 0(y-0) + 1(z-0) = 0$ $z = 0$. So, the equation of plane $P$ is $z=0$.

We are given the point $M(1,0,1)$. We need to find the foot of the perpendicular drawn from $M$ to the plane $P$ ($z=0$). Let the foot of the perpendicular be $Q(\alpha, \beta, \lambda)$. The line passing through $M(1,0,1)$ and perpendicular to the plane $z=0$ has a direction vector parallel to the normal vector of the plane, which is $\hat{k}$. The equation of this line is $\vec{r} = \vec{OM} + t\vec{n} = (1\hat{i} + 0\hat{j} + 1\hat{k}) + t(0\hat{i} + 0\hat{j} + 1\hat{k}) = \hat{i} + (1+t)\hat{k}$. A general point on this line is $(1, 0, 1+t)$.

The foot of the perpendicular $Q$ is the point where this line intersects the plane $z=0$. The z-coordinate of $Q$ must satisfy the plane equation. So, $1+t = 0 \implies t = -1$. Substitute $t=-1$ into the coordinates of the general point on the line to find the coordinates of $Q$: $Q = (1, 0, 1+(-1)) = (1, 0, 0)$.

The coordinates of $Q$ are given as $(\alpha, \beta, \lambda)$. Comparing $Q(1,0,0)$ with $Q(\alpha, \beta, \lambda)$, we have: $\alpha = 1$ $\beta = 0$ $\lambda = 0$

We need to find the value of $3(\alpha+\beta+\lambda)$. $3(\alpha+\beta+\lambda) = 3(1+0+0) = 3(1) = 3$.