Question

Let $A = \left\{ (x, y) \in R \times R : |\sin x|. \sin y = \frac{-1}{4} \right\}$

$B = \left\{ (x, y) \in R \times R : \cos(x+y) + \cos(x - y) = \frac{3}{2} \right\}$

$C = \left\{ (x, y) \in R \times R : 0 < x < 2\pi \ \& \ \pi < y < 2\pi \right\}$

Then $|A \cap B \cap C|$ is

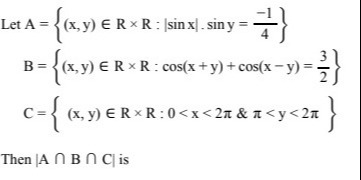
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (D)

4

Answer 2

1. Simplify Set B: The identity $\cos(x+y) + \cos(x - y) = 2 \cos x \cos y$ is used. So, $2 \cos x \cos y = \frac{3}{2}$, which simplifies to $\cos x \cos y = \frac{3}{4}$.

2. Combine Conditions from A and B:

   • From Set A: $|\sin x| \sin y = -\frac{1}{4}$. Squaring both sides gives $\sin^2 x \sin^2 y = \frac{1}{16}$.
   • Using $\sin^2 \theta = 1 - \cos^2 \theta$, we get $(1 - \cos^2 x)(1 - \cos^2 y) = \frac{1}{16}$.
   • Expanding this, we have $1 - (\cos^2 x + \cos^2 y) + \cos^2 x \cos^2 y = \frac{1}{16}$.
   • From Set B, $\cos x \cos y = \frac{3}{4}$, so $\cos^2 x \cos^2 y = \left(\frac{3}{4}\right)^2 = \frac{9}{16}$.
   • Substituting this into the expanded equation: $1 - (\cos^2 x + \cos^2 y) + \frac{9}{16} = \frac{1}{16}$.
   • This simplifies to $\cos^2 x + \cos^2 y = 1 + \frac{8}{16} = \frac{3}{2}$.

3. Solve for $\cos^2 x$ and $\cos^2 y$:

   • Let $u = \cos^2 x$ and $v = \cos^2 y$. We have the system: $u + v = \frac{3}{2}$ $uv = \frac{9}{16}$
   • These are the roots of the quadratic equation $t^2 - \frac{3}{2}t + \frac{9}{16} = 0$, which is equivalent to $16t^2 - 24t + 9 = 0$ or $(4t - 3)^2 = 0$.
   • The only solution is $t = \frac{3}{4}$. Thus, $\cos^2 x = \frac{3}{4}$ and $\cos^2 y = \frac{3}{4}$.

4. Derive $|\sin x|$ and $\sin y$:

   • If $\cos^2 x = \frac{3}{4}$, then $\sin^2 x = 1 - \frac{3}{4} = \frac{1}{4}$, so $|\sin x| = \frac{1}{2}$.
   • If $\cos^2 y = \frac{3}{4}$, then $\sin^2 y = 1 - \frac{3}{4} = \frac{1}{4}$, so $|\sin y| = \frac{1}{2}$.
   • Substitute $|\sin x| = \frac{1}{2}$ into Set A's condition: $\frac{1}{2} \sin y = -\frac{1}{4}$, which gives $\sin y = -\frac{1}{2}$. This is consistent with $|\sin y| = \frac{1}{2}$.

5. Find possible values for $x$ and $y$ within Set C:

   • Set C requires $0 < x < 2\pi$ and $\pi < y < 2\pi$.

   • For $\sin y = -\frac{1}{2}$ and $y \in (\pi, 2\pi)$, the possible values for $y$ are $y = \frac{7\pi}{6}$ (3rd quadrant) and $y = \frac{11\pi}{6}$ (4th quadrant).

   • Case 1: $y = \frac{7\pi}{6}$

     • $\cos y = \cos(\frac{7\pi}{6}) = -\frac{\sqrt{3}}{2}$.
     • From $\cos x \cos y = \frac{3}{4}$, we have $\cos x (-\frac{\sqrt{3}}{2}) = \frac{3}{4}$, so $\cos x = -\frac{\sqrt{3}}{2}$.
     • For $\cos x = -\frac{\sqrt{3}}{2}$ and $x \in (0, 2\pi)$, the possible values for $x$ are $x = \frac{5\pi}{6}$ and $x = \frac{7\pi}{6}$.
     • We must check if $|\sin x| = \frac{1}{2}$ for these values:
       • For $x = \frac{5\pi}{6}$, $|\sin(\frac{5\pi}{6})| = |\frac{1}{2}| = \frac{1}{2}$. Valid.
       • For $x = \frac{7\pi}{6}$, $|\sin(\frac{7\pi}{6})| = |-\frac{1}{2}| = \frac{1}{2}$. Valid.
     • This gives two points: $(\frac{5\pi}{6}, \frac{7\pi}{6})$ and $(\frac{7\pi}{6}, \frac{7\pi}{6})$. Both satisfy $0 < x < 2\pi$ and $\pi < y < 2\pi$.

   • Case 2: $y = \frac{11\pi}{6}$

     • $\cos y = \cos(\frac{11\pi}{6}) = \frac{\sqrt{3}}{2}$.
     • From $\cos x \cos y = \frac{3}{4}$, we have $\cos x (\frac{\sqrt{3}}{2}) = \frac{3}{4}$, so $\cos x = \frac{\sqrt{3}}{2}$.
     • For $\cos x = \frac{\sqrt{3}}{2}$ and $x \in (0, 2\pi)$, the possible values for $x$ are $x = \frac{\pi}{6}$ and $x = \frac{11\pi}{6}$.
     • We must check if $|\sin x| = \frac{1}{2}$ for these values:
       • For $x = \frac{\pi}{6}$, $|\sin(\frac{\pi}{6})| = |\frac{1}{2}| = \frac{1}{2}$. Valid.
       • For $x = \frac{11\pi}{6}$, $|\sin(\frac{11\pi}{6})| = |-\frac{1}{2}| = \frac{1}{2}$. Valid.
     • This gives two points: $(\frac{\pi}{6}, \frac{11\pi}{6})$ and $(\frac{11\pi}{6}, \frac{11\pi}{6})$. Both satisfy $0 < x < 2\pi$ and $\pi < y < 2\pi$.

6. Conclusion:

   • In total, there are 4 points in the intersection $A \cap B \cap C$: $(\frac{5\pi}{6}, \frac{7\pi}{6})$, $(\frac{7\pi}{6}, \frac{7\pi}{6})$, $(\frac{\pi}{6}, \frac{11\pi}{6})$, and $(\frac{11\pi}{6}, \frac{11\pi}{6})$.
   • Therefore, $|A \cap B \cap C| = 4$.