Question

Let A = \left\\{ {1,2,3} \right\\},B = \left\\{ {4,5,6,7} \right\\} and let f = \left\\{ {\left( {1,4} \right),\left( {2,5} \right),\left( {3,6} \right)} \right\\} be a function from A to B. State whether f is one-one.

Answer 1

First draw the mapping of the function $f$. After that check whether the function $f$ follows the definition of a one-one function or not. If it follows it is a one-one function else it is not a one-one function.

Complete step-by-step solution:
First, let us know that it is a one-one function.
One to one function denotes the mapping of two sets. A function g is one-to-one if every element of the range of g corresponds to exactly one element of the domain of g. One-to-one is also written as 1-1. A function f() is a method, which relates elements/values of one variable to the elements/values of another variable, in such a way that the elements of the first variable identically determine the elements of the second variable.
The mapping of the function $f$ is given below.

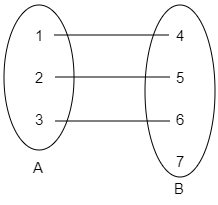
According to the question,
$f:A \to B$ is defined as f = \left\\{ {\left( {1,4} \right),\left( {2,5} \right),\left( {3,6} \right)} \right\\}
Which means,
$\Rightarrow f\left( 1 \right) = 4,f\left( 2 \right) = 5,f\left( 3 \right) = 6$
As, It is seen that the images of distinct elements of A under f are distinct, which follows the definition of the one-one function.

Hence, the function $f$ is one-one.

Note: A function is a relation that describes that there should be only one output for each input. OR we can say that a special kind of relation (a set of ordered pairs) which follows a rule i.e every X-value should be associated with only one y-value is called a Function.
To recall, a function is something, which relates elements/values of one set to the elements/values of another set, in such a way that elements of the second set are identically determined by the elements of the first set. A function has many types that define the relationship between two sets in a different pattern. There are various types of functions as one to one function, onto function, many to one function, etc.
A function has many types and one of the most common functions used is the one-to-one function or injective function. Also, we will be learning here the inverse of this function.