Question

Let A=\left\\{ 0,1,2,3 \right\\}\text{ and }B=\left\\{ 1,3,5,7,9 \right\\} be two sets. Let $f:A\to B$ be a function given by $f\left( x \right)=2x+1$ . Represent this function as a set of ordered pairs.

Answer 1

First, we will start by defining what are sets and functions. Finally, we will define what are ordered pairs and the set of ordered pairs. We will then take two sets from the question and we will put the input values from set $A$ and get resultant value and form the coordinates and ultimately form a set and get the answer.

Complete step-by-step answer:
First, we will define what a set is. So, a set is simply a collection of things. For example, a set of whole numbers: \left\\{ 0,1,2,3,..... \right\\} and a set of prime numbers will be: \left\\{ 2,3,5,7,11,..... \right\\} . We now need some notation to make sets easier. Consider, a\in \left\\{ a,b,c \right\\} , this means that $a$ is the set containing the elements $a,b\text{ and }c$ . We will use curly braces \left\\{ {} \right\\} to enclose elements of a set.
Now, a function relates inputs to outputs. A function takes elements from a set which is also called the domain and relates them to elements in a set that is the co-domain. All the outputs that are the actual values produced by the function together is called the range. So overall, a function is a special type of relation where every element in the domain is included, and any input produces only one output.
Finally, let’s understand the meaning of ordered pairs. So, an ordered pair is a composition of the $x$ coordinate (abscissa) and the $y$ coordinate (ordinate), having two values written in a fixed order within parentheses. It helps to locate a point on the Cartesian plane for better visual comprehension.
A function can then be defined as a set of ordered pairs: For example: \left\\{ \left( 2,4 \right),\left( 3,5 \right),\left( 7,3 \right) \right\\} is a function that says: $2$ is related to $4$, $3$ is related to $5$ , $7$ is related to $3$ .
Now, we are given the sets: A=\left\\{ 0,1,2,3 \right\\}\text{ and }B=\left\\{ 1,3,5,7,9 \right\\} and a function $f:A\to B$ , so set$A$ is an input and $B$ will be the set of output.
Now we have: $f\left( x \right)=2x+1$ , we will now put the input values from $A$ that means we will be putting values from set $A$ into the given function. So,
$\begin{aligned} & f\left( 0 \right)=2\left( 0 \right)+1=0+1=1\Rightarrow \left( 0,1 \right) \\\ & f\left( 1 \right)=2\left( 1 \right)+1=2+1=3\Rightarrow \left( 1,3 \right) \\\ & f\left( 2 \right)=2\left( 2 \right)+1=4+1=5\Rightarrow \left( 2,5 \right) \\\ & f\left( 3 \right)=2\left( 3 \right)+1=6+1=7\Rightarrow \left( 3,7 \right) \\\ \end{aligned}$
Now the set of ordered pairs will be: f:\left\\{ \left( 0,1 \right),\left( 1,3 \right),\left( 2,5 \right),\left( 3,7 \right) \right\\}
Now, an arrow diagram for these ordered pairs is as follows:

Let’s plot these points from the set f:\left\\{ \left( 0,1 \right),\left( 1,3 \right),\left( 2,5 \right),\left( 3,7 \right) \right\\} on graph:

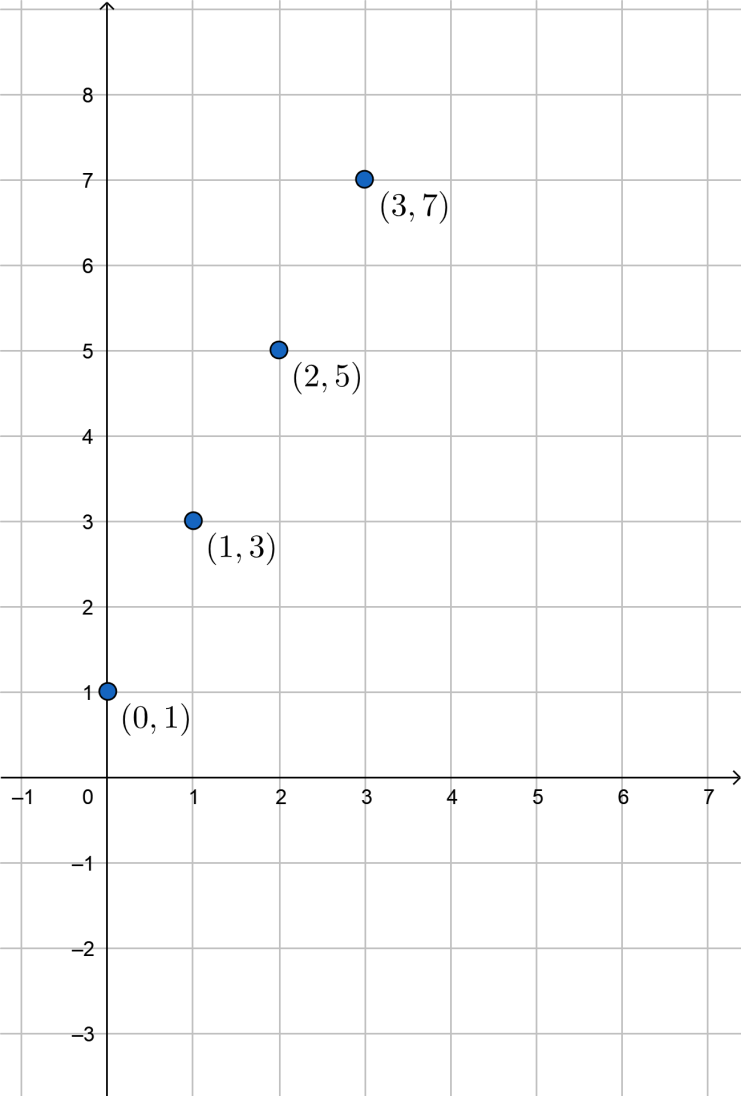
Therefore, the answer is: f:\left\\{ \left( 0,1 \right),\left( 1,3 \right),\left( 2,5 \right),\left( 3,7 \right) \right\\}

Note: As the name “ordered pair” suggests, the order in which values are written in a pair is very important for example the ordered pair $\left( 6,4 \right)$ is different from the pair $\left( 4,6 \right)$ . Both represent two different points. The coordinate geometry uses ordered pairs to represent geometric figures and objects in an open space for visual comprehension. Geometric shapes like circle, triangle, square, rectangle and polygons use the ordered pairs to represent the center, vertices and the length of the sides with coordinates.