Solveeit Logo
Login

Question

Question: Let $a-\frac{1}{b}$, $b-\frac{1}{c}$ and $c-\frac{1}{a}$ be the roots of the cubic equation $x^3-5x^...

Let a−1ba-\frac{1}{b}, b−1cb-\frac{1}{c} and c−1ac-\frac{1}{a} be the roots of the cubic equation x3−5x2−15x+3=0x^3-5x^2-15x+3=0 (where a,b,c∈Ra,b,c \in R, a,b,ca,b,c are non-zero numbers and RR is the set of all real numbers). Then, the sum of all the possible value(s) of abcabc is

Answer

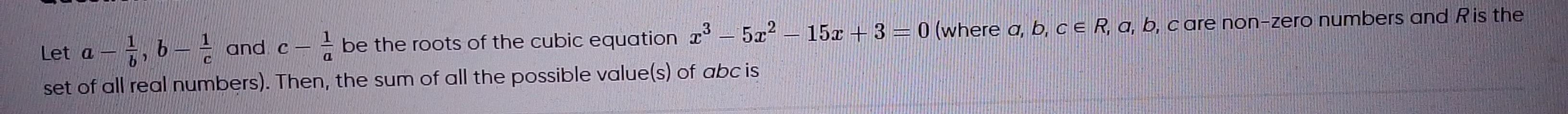
2

Explanation

Solution

Let the given cubic equation be x3−5x2−15x+3=0x^3-5x^2-15x+3=0. Let its roots be r1,r2,r3r_1, r_2, r_3. According to Vieta's formulas:

  1. Sum of the roots: r1+r2+r3=−(−5)/1=5r_1+r_2+r_3 = -(-5)/1 = 5
  2. Sum of the product of roots taken two at a time: r1r2+r2r3+r3r1=−15/1=−15r_1r_2+r_2r_3+r_3r_1 = -15/1 = -15
  3. Product of the roots: r1r2r3=−(3)/1=−3r_1r_2r_3 = -(3)/1 = -3

We are given that the roots are a−1ba-\frac{1}{b}, b−1cb-\frac{1}{c}, and c−1ac-\frac{1}{a}. Let's use the sum of the roots: r1+r2+r3=(a−1b)+(b−1c)+(c−1a)=5r_1+r_2+r_3 = \left(a-\frac{1}{b}\right) + \left(b-\frac{1}{c}\right) + \left(c-\frac{1}{a}\right) = 5 Rearranging the terms, we get: (a+b+c)−(1a+1b+1c)=5(a+b+c) - \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) = 5 (Equation 1)

Now, let's use the product of the roots: r1r2r3=(a−1b)(b−1c)(c−1a)=−3r_1r_2r_3 = \left(a-\frac{1}{b}\right)\left(b-\frac{1}{c}\right)\left(c-\frac{1}{a}\right) = -3 Let's expand the product: First, expand (a−1b)(b−1c)(a-\frac{1}{b})(b-\frac{1}{c}): (a−1b)(b−1c)=ab−ac−1+1bc(a-\frac{1}{b})(b-\frac{1}{c}) = ab - \frac{a}{c} - 1 + \frac{1}{bc} Now, multiply this by (c−1a)(c-\frac{1}{a}): (ab−ac−1+1bc)(c−1a)\left(ab - \frac{a}{c} - 1 + \frac{1}{bc}\right)\left(c - \frac{1}{a}\right) =abc−b−a+1c−c+1a+1b−1abc= abc - b - a + \frac{1}{c} - c + \frac{1}{a} + \frac{1}{b} - \frac{1}{abc} Rearranging the terms: =abc−(a+b+c)+(1a+1b+1c)−1abc= abc - (a+b+c) + \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) - \frac{1}{abc}

So, we have the equation: abc−(a+b+c)+(1a+1b+1c)−1abc=−3abc - (a+b+c) + \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) - \frac{1}{abc} = -3 (Equation 2)

Let P=abcP = abc. From Equation 1, we know that (a+b+c)−(1a+1b+1c)=5(a+b+c) - \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) = 5. Notice that the term in Equation 2, −(a+b+c)+(1a+1b+1c)-(a+b+c) + \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right), is the negative of Equation 1's left side. So, −(a+b+c)+(1a+1b+1c)=−5-(a+b+c) + \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) = -5.

Substitute this into Equation 2: P−5−1P=−3P - 5 - \frac{1}{P} = -3 P−1P=2P - \frac{1}{P} = 2

Since a,b,ca,b,c are non-zero, P=abc≠0P = abc \neq 0. We can multiply the equation by PP: P2−1=2PP^2 - 1 = 2P P2−2P−1=0P^2 - 2P - 1 = 0

This is a quadratic equation for PP. We can solve for PP using the quadratic formula P=−B±B2−4AC2AP = \frac{-B \pm \sqrt{B^2-4AC}}{2A}: P=−(−2)±(−2)2−4(1)(−1)2(1)P = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(-1)}}{2(1)} P=2±4+42P = \frac{2 \pm \sqrt{4 + 4}}{2} P=2±222P = \frac{2 \pm 2\sqrt{2}}{2} P=2±222P = \frac{2 \pm 2\sqrt{2}}{2} P=1±2P = 1 \pm \sqrt{2}

Thus, there are two possible values for abcabc: P1=1+2P_1 = 1+\sqrt{2} and P2=1−2P_2 = 1-\sqrt{2}. The question asks for the sum of all possible values of abcabc. Sum of possible values =P1+P2=(1+2)+(1−2)=1+1=2= P_1 + P_2 = (1+\sqrt{2}) + (1-\sqrt{2}) = 1+1 = 2.

The existence of such real numbers a,b,ca,b,c is consistent with the fact that the given cubic equation x3−5x2−15x+3=0x^3-5x^2-15x+3=0 has three real roots (which can be verified by checking the local maximum and minimum values of the function f(x)=x3−5x2−15x+3f(x)=x^3-5x^2-15x+3).