Question

Let a focal chord of the parabola ${{y}^{2}}=16x$ cuts it at points $\left( f,g \right)$ and $\left( h,k \right)$. Then $f.h$ is:
A. -8
B. -16
C. 16
D. None of these

Answer 1

We here need to find $f.h$ , i.e. the product of the x-coordinates of the extremities of the focal chord of the given parabola. For this, we will first write the given coordinates in the parametric form and, i.e. $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ and hence write the product in the parametric form. Then we will use the property of ${{t}_{1}}{{t}_{2}}=-1$ where ${{t}_{1}}$ and ${{t}_{2}}$ are the parameters for the extremities of the focal chord. We will then put this value in the required product and hence we will get our result.

Complete step-by-step solution
Now, we have been given the two points the focal chord of the parabola ${{y}^{2}}=16x$ passes through. A focal chord of a parabola is the chord, which passes through its focus.

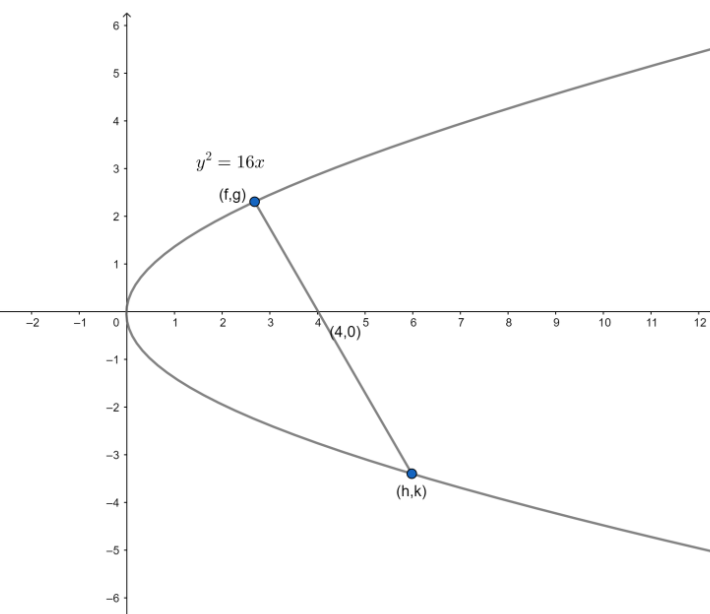
The parabola ${{y}^{2}}=16x$ is in the form of ${{y}^{2}}=4ax$ where the focus is $\left( a,0 \right)$ . thus, we can write the given parabola as:
$\begin{aligned} & {{y}^{2}}=16x \\\ & \Rightarrow {{y}^{2}}=4.4x \\\ \end{aligned}$
Thus, for the given parabola, $a=4$
Now, any point on a parabola ${{y}^{2}}=4ax$ is given by $\left( a{{t}^{2}},2at \right)$ where ‘t’ is a parameter.
As mentioned above, here $a=4$
Thus, we can take the given points $\left( f,g \right)$ and $\left( h,k \right)$ as $\left( 4{{t}_{1}}^{2},8{{t}_{1}} \right)$ and $\left( 4{{t}_{2}}^{2},8{{t}_{2}} \right)$ respectively where $'{{t}_{1}}'$ and $'{{t}_{2}}'$ are two different parameters.
Thus, we get:
$f=4{{t}_{1}}^{2}$
$h=4{{t}_{2}}^{2}$
So we can get $f.h$ as by multiplying these both.
Thus, we get:
$\begin{aligned} & f.h=4{{t}_{1}}^{2}.4{{t}_{2}}^{2} \\\ & \Rightarrow f.h=16{{t}_{1}}^{2}{{t}_{2}}^{2} \\\ \end{aligned}$
$\Rightarrow f.h=16{{\left( {{t}_{1}}{{t}_{2}} \right)}^{2}}$ ……(i)
Now, we know that if the focal chord of a parabola of the type ${{y}^{2}}=4ax$ passes through the points $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ then the relation between the points is given by:
${{t}_{1}}{{t}_{2}}=-1$
Thus, by putting this value, we can find the value of $f.h$
Now, putting this value in equation (i) we get:
$\begin{aligned} & f.h=16{{\left( {{t}_{1}}{{t}_{2}} \right)}^{2}} \\\ & \Rightarrow f.h=16{{\left( -1 \right)}^{2}} \\\ & \Rightarrow f.h=16\left( 1 \right) \\\ & \Rightarrow f.h=16 \\\ \end{aligned}$
Thus option (C) is the correct option.

Note: We have obtained the result ${{t}_{1}}{{t}_{2}}=-1$ by the following method:
In the given figure, we have a parabola ${{y}^{2}}=4ax$ with the focus at S. The extremities of the chord are P and Q.

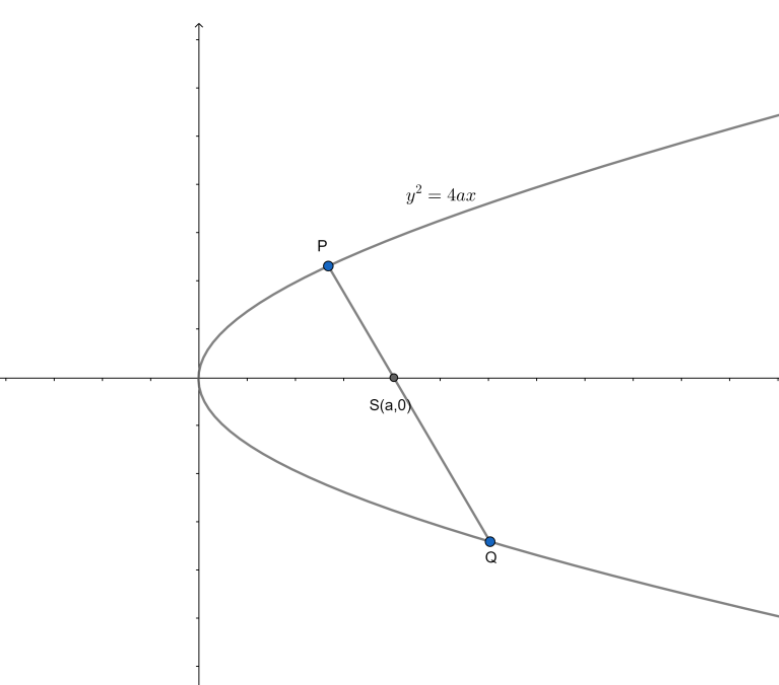
Let the point P be $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and let the point Q be $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$.
Hence, the equation through point P and Q will be:
$\begin{aligned} & y-2a{{t}_{1}}=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{a{{t}_{2}}^{2}-a{{t}_{1}}^{2}}\left( x-a{{t}_{1}}^{2} \right) \\\ & y-2a{{t}_{1}}=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}\left( x-a{{t}_{1}}^{2} \right) \\\ \end{aligned}$
Now, this line passes through the focus, i.e. S (a,0)
Putting this point in the equation of the chord we get:

& y-2a{{t}_{1}}=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}\left( x-a{{t}_{1}}^{2} \right) \\\ & \Rightarrow 0-2a{{t}_{1}}=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}\left( a-a{{t}_{1}}^{2} \right) \\\ & \Rightarrow -2a{{t}_{1}}=\dfrac{2a}{{{t}_{2}}+{{t}_{1}}}\left( 1-{{t}_{1}}^{2} \right) \\\ & \Rightarrow -{{t}_{1}}=\dfrac{1-{{t}_{1}}^{2}}{{{t}_{2}}+{{t}_{1}}} \\\ & \Rightarrow -{{t}_{1}}{{t}_{2}}-{{t}_{1}}^{2}=1-{{t}_{1}}^{2} \\\ & \Rightarrow -{{t}_{1}}{{t}_{2}}=1-{{t}_{1}}^{2}+{{t}_{1}}^{2} \\\ & \Rightarrow -{{t}_{1}}{{t}_{2}}=1 \\\ & \Rightarrow {{t}_{1}}{{t}_{2}}=-1 \\\ \end{aligned}$$