Question

Let $A\equiv \left( 3,2 \right);B\equiv \left( 5,1 \right)$ . $ABP$ is an equilateral triangle constructed on the side of $AB$ remote from the origin then the orthocentre of the triangle $ABP$ is:
(a) $\left( 4-\dfrac{1}{2}\sqrt{3},\dfrac{3}{2}-\sqrt{3} \right)$
(b) $\left( 4+\dfrac{1}{2}\sqrt{3},\dfrac{3}{2}+\sqrt{3} \right)$
(c) $\left( 4-\dfrac{1}{6}\sqrt{3},\dfrac{3}{2}-\dfrac{1}{3}\sqrt{3} \right)$
(d) $\left( 4+\dfrac{1}{6}\sqrt{3},\dfrac{3}{2}+\dfrac{1}{3}\sqrt{3} \right)$

Answer 1

Hint: For solving this question we will find the coordinates of the midpoint $C\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ of the side AB of the triangle using the midpoint formula $C\equiv \left( \dfrac{{{x}_{A}}+{{x}_{B}}}{2},\dfrac{{{y}_{A}}+{{y}_{B}}}{2} \right)$ and from the geometrical property of the equilateral triangle we will find the length of the $CP=r$ . After that, we will find the slope $\tan \theta$ of the line CP and then, find the value of $\sin \theta$ and $\cos \theta$ . After that, we will use the formula $P\equiv \left( {{x}_{1}}+r\cos \theta ,{{y}_{1}}+r\sin \theta \right)$ to find the coordinates of the point P . Then, we will directly apply the formula $O\equiv \left( \dfrac{{{x}_{A}}+{{x}_{B}}+{{x}_{P}}}{3},\dfrac{{{y}_{A}}+{{y}_{B}}+{{y}_{P}}}{3} \right)$ for the orthocentre of an equilateral triangle $ABP$ , and we will get the correct answer.

Complete step-by-step answer:

Given: It is given that $ABP$ is an equilateral triangle constructed on the side of $AB$ remote from the origin and $A\equiv \left( 3,2 \right);B\equiv \left( 5,1 \right)$ .
Now, we will use the following formulas of co-ordinate geometry to solve this question. Formulas are listed below:
1. If $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ then, coordinates of the midpoint of segment AB will be $C\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ .
2. The slope of line AB through points $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ is ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\tan \theta$ , where $\theta$ is the angle between a line through A and B and the positive x-axis in an anticlockwise sense.
3. If two lines are perpendicular then the product of their slopes will be equal to -1.
4. Distance between point $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ can be calculated by the distance formula as $AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ .
5. The coordinates of any point on the line at a distance $r$ from the given point $C\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ are $P\equiv \left( {{x}_{1}}+r\cos \theta ,{{y}_{1}}+r\sin \theta \right)$ . If P is on the right side of C, then $r$ is positive and if P is on the left side of C, then $r$ is negative.
6. For an equilateral triangle, ABC where $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ , $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ and $C\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ . Then, coordinates of its orthocentre O will be $O\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
Now, we come back to our problem, in which $\Delta ABP$ is an equilateral triangle then, all angle of the triangle will be of ${{60}^{0}}$ . Using the formula written in the first point to find the coordinates of the midpoint of AB as we know that $A\equiv \left( 3,2 \right);B\equiv \left( 5,1 \right)$ . Then,
$\begin{aligned} & C\equiv \left( \dfrac{5+3}{2},\dfrac{2+1}{2} \right) \\\ & \Rightarrow C\equiv \left( 4,\dfrac{3}{2} \right) \\\ \end{aligned}$
Now, using the formula written in the fourth point length of side AB $=\sqrt{{{\left( 5-3 \right)}^{2}}+{{\left( 1-2 \right)}^{2}}}=\sqrt{5}$ . And as the $\Delta ABP$ is an equilateral triangle then, length of all sides will be $\sqrt{5}$ .
Now, using the formula written in the second point, slope of the line through AB is ${{m}_{AB}}=\dfrac{1-2}{5-3}=-\dfrac{1}{2}$ .
Now, we can plot the figure of the $\Delta ABP$ . The figure is given below:

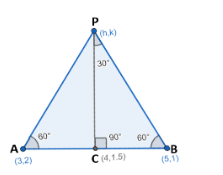
Now, from the above plot, we can say that as the $\Delta ABP$ is an equilateral triangle the PC will be perpendicular to the AB then, from the third point we can find the slope of PB will be $-\dfrac{1}{{{m}_{AB}}}=2$ .
Now, if $\theta$ is the angle made by line through PC and positive x-axis so, $\tan \theta =2$ . Then,
$\begin{aligned} & \tan \theta =2 \\\ & \Rightarrow \cos \theta =\dfrac{1}{\sqrt{1+{{\tan }^{2}}\theta }}=\dfrac{1}{\sqrt{5}}............\left( 1 \right) \\\ & \Rightarrow \sin \theta =\tan \theta \times \cos \theta =\dfrac{2}{\sqrt{5}}.............\left( 2 \right) \\\ \end{aligned}$
Now, in the above figure, we can write that length PC is equal to $\left( AP \right)\sin {{60}^{0}}=\dfrac{\sqrt{15}}{2}$ . So, now on the line through PC we know that $C\equiv \left( 4,\dfrac{3}{2} \right)$ and P is on the right side of the point C at a distance of $r=\dfrac{\sqrt{15}}{2}$ . Then, with the help of the formula written in the 5th point $P\equiv \left( {{x}_{1}}+r\cos \theta ,{{y}_{1}}+r\sin \theta \right)$ . Where, $\cos \theta =\dfrac{1}{\sqrt{5}}$ and $\sin \theta =\dfrac{2}{\sqrt{5}}$ . Then,
$\begin{aligned} & P\equiv \left( {{x}_{1}}+r\cos \theta ,{{y}_{1}}+r\sin \theta \right) \\\ & \Rightarrow P\equiv \left( 4+\dfrac{\sqrt{15}}{2}\times \dfrac{1}{\sqrt{5}},\dfrac{3}{2}+\dfrac{\sqrt{15}}{2}\times \dfrac{2}{\sqrt{5}} \right) \\\ & \Rightarrow P\equiv \left( 4+\dfrac{\sqrt{3}}{2},\dfrac{3}{2}+\sqrt{3} \right) \\\ \end{aligned}$
Now, we have the coordinates of all three points of the equilateral triangle ABP as follow:
$A\equiv \left( 3,2 \right);B\equiv \left( 5,1 \right):P\left( 4+\dfrac{\sqrt{3}}{2},\dfrac{3}{2}+\sqrt{3} \right)$
Now, using the formula written in the sixth point we can find the coordinates of the orthocentre O of the triangle ABP. Then,
$\begin{aligned} & O\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \\\ & \Rightarrow O\equiv \left( \dfrac{12+\dfrac{\sqrt{3}}{2}}{3},\dfrac{\dfrac{9}{2}+\sqrt{3}}{3} \right) \\\ & \Rightarrow O\equiv \left( 4+\dfrac{\sqrt{3}}{6},\dfrac{3}{2}+\dfrac{\sqrt{3}}{3} \right) \\\ \end{aligned}$
Thus, from the above result, we can say that coordinates of the required point will be $\left( 4+\dfrac{\sqrt{3}}{6},\dfrac{3}{2}+\dfrac{\sqrt{3}}{3} \right)$ .
Hence, (d) is the correct result.

Note: Here, the student must proceed stepwise in the solution and if you use the parametric form of the straight line as we used in this solution then, the calculation will be minimum. Moreover, we should not confuse between option (c) and (d) as it is given in the question that point P will be on the remote side of the origin then, we will take the positive value of $r$ for finding the coordinates of point P and avoid making calculation mistakes while solving.