Question

Let $A = \begin{pmatrix} x^2 & 6 & 8 \\ 3 & y^2 & 9 \\ 4 & 5 & z^2 \end{pmatrix}$, $B = \begin{pmatrix} 2x & 3 & 5 \\ 2 & 2y & 6 \\ 1 & 4 & 2z-3 \end{pmatrix}$ be two matrices and if Tr. (A) = Tr. (B), then the value of (x+y+z) is equal to

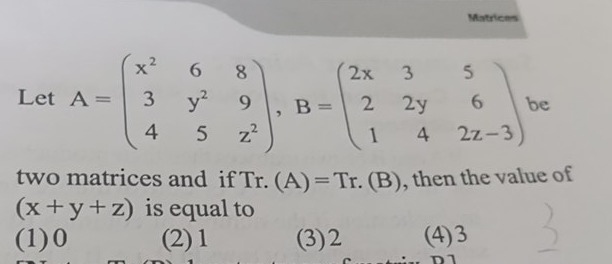
• A. 0
• B. 1
• C. 2
• D. 3

Answer 1

Answer: (D)

3

Answer 2

Let the given matrices be $A = \begin{pmatrix} x^2 & 6 & 8 \\ 3 & y^2 & 9 \\ 4 & 5 & z^2 \end{pmatrix}$ and $B = \begin{pmatrix} 2x & 3 & 5 \\ 2 & 2y & 6 \\ 1 & 4 & 2z-3 \end{pmatrix}$.

The trace of a square matrix is the sum of the elements on the main diagonal.

The trace of matrix A is Tr(A) = $x^2 + y^2 + z^2$.

The trace of matrix B is Tr(B) = $2x + 2y + (2z-3)$.

According to the problem statement, Tr(A) = Tr(B). Therefore, we have the equation: $x^2 + y^2 + z^2 = 2x + 2y + 2z - 3$

Rearrange the terms to one side to form an equation equal to zero: $x^2 - 2x + y^2 - 2y + z^2 - 2z + 3 = 0$

We can complete the square for the terms involving x, y, and z. For the x terms: $x^2 - 2x$. We add and subtract $(2/2)^2 = 1^2 = 1$. So, $x^2 - 2x + 1 = (x-1)^2$. For the y terms: $y^2 - 2y$. We add and subtract $(2/2)^2 = 1^2 = 1$. So, $y^2 - 2y + 1 = (y-1)^2$. For the z terms: $z^2 - 2z$. We add and subtract $(2/2)^2 = 1^2 = 1$. So, $z^2 - 2z + 1 = (z-1)^2$.

Substitute these completed squares back into the equation: $(x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - 2z + 1) = 0$ This simplifies to: $(x-1)^2 + (y-1)^2 + (z-1)^2 = 0$

Assuming x, y, and z are real numbers, the square of a real number is always non-negative. The sum of non-negative terms is zero if and only if each term is zero. Therefore, we must have: $(x-1)^2 = 0 \implies x-1 = 0 \implies x = 1$ $(y-1)^2 = 0 \implies y-1 = 0 \implies y = 1$ $(z-1)^2 = 0 \implies z-1 = 0 \implies z = 1$

We are asked to find the value of (x+y+z). x + y + z = 1 + 1 + 1 = 3.