Question

Let

$A = \begin{pmatrix} 1 & 0 & -1 \\ 0 & 2 & 2 \\ 1 & 1 & 3 \end{pmatrix}$. If B = adj. A, C = A$^{-1}$ and

$N = \frac{|adj. B|}{|C|}$ then the sum of all the divisors of 'N' which are divisible by 6 is

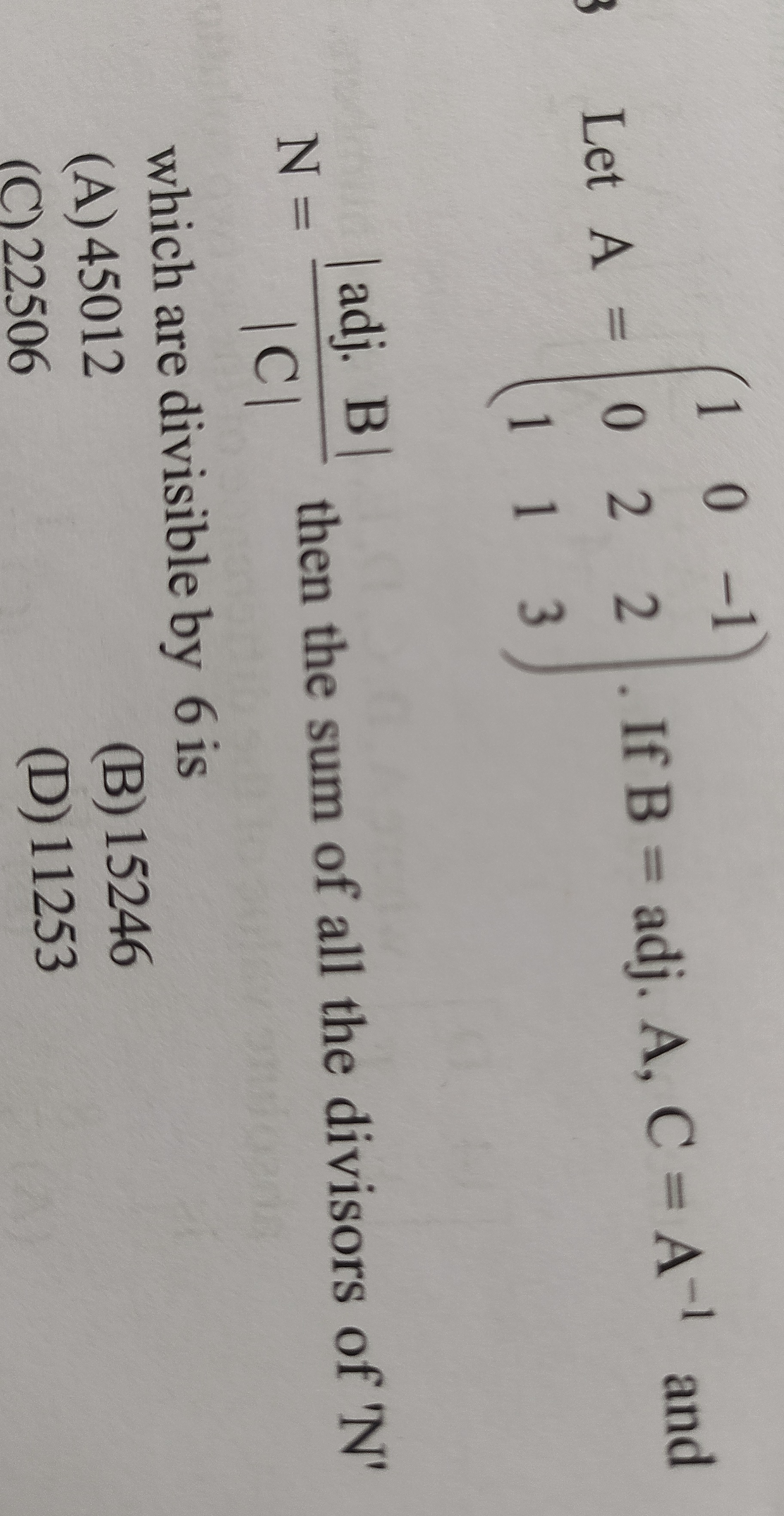
• A. 45012
• B. 15246
• C. 22506
• D. 11253

Answer 1

Answer: (C)

22506

Answer 2

Let $A = \begin{pmatrix} 1 & 0 & -1 \\ 0 & 2 & 2 \\ 1 & 1 & 3 \end{pmatrix}$. We are given $B = \text{adj. A}$ and $C = A^{-1}$. We need to calculate $N = \frac{|\text{adj. B}|}{|C|}$.

First, let's find the determinant of matrix A, denoted by $|A|$. $|A| = \begin{vmatrix} 1 & 0 & -1 \\ 0 & 2 & 2 \\ 1 & 1 & 3 \end{vmatrix}$ Expanding along the first row: $|A| = 1 \cdot \begin{vmatrix} 2 & 2 \\ 1 & 3 \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 2 \\ 1 & 3 \end{vmatrix} + (-1) \cdot \begin{vmatrix} 0 & 2 \\ 1 & 1 \end{vmatrix}$ $|A| = 1 \cdot (2 \cdot 3 - 2 \cdot 1) - 0 + (-1) \cdot (0 \cdot 1 - 2 \cdot 1)$ $|A| = (6 - 2) - (0 - 2) = 4 - (-2) = 4 + 2 = 6$. So, $|A| = 6$.

For a square matrix A of order $n$, we have the following properties:

1. $|\text{adj. A}| = |A|^{n-1}$
2. $|A^{-1}| = \frac{1}{|A|}$
3. $\text{adj. (adj. A)} = |A|^{n-2} A$
4. $|\text{adj. (adj. A)}| = ||A|^{n-2} A| = (|A|^{n-2})^n |A| = |A|^{n(n-2)+1} = |A|^{n^2-2n+1} = |A|^{(n-1)^2}$

In this problem, the order of matrix A is $n=3$. $B = \text{adj. A}$, so $|\text{adj. B}| = |\text{adj. (adj. A)}|$. Using property 4 with $n=3$: $|\text{adj. (adj. A)}| = |A|^{(3-1)^2} = |A|^4$.

$C = A^{-1}$. Using property 2: $|C| = |A^{-1}| = \frac{1}{|A|}$.

Now we can calculate N: $N = \frac{|\text{adj. B}|}{|C|} = \frac{|A|^4}{1/|A|} = |A|^4 \cdot |A| = |A|^5$. Since $|A| = 6$, we have $N = 6^5$.

We need to find the sum of all divisors of $N = 6^5$ which are divisible by 6. First, find the prime factorization of N: $N = 6^5 = (2 \times 3)^5 = 2^5 \times 3^5$.

A divisor of N is of the form $d = 2^a \times 3^b$, where $0 \le a \le 5$ and $0 \le b \le 5$. A divisor $d$ is divisible by 6 if it is divisible by both 2 and 3. This means the exponent of 2 in its prime factorization must be at least 1, and the exponent of 3 must be at least 1. So, the divisors of N divisible by 6 are of the form $2^a \times 3^b$, where $1 \le a \le 5$ and $1 \le b \le 5$.

The sum of these divisors is the sum of all terms $2^a \times 3^b$ for $a \in \{1, 2, 3, 4, 5\}$ and $b \in \{1, 2, 3, 4, 5\}$. This sum can be factored as the product of two sums: Sum $= \left( \sum_{a=1}^{5} 2^a \right) \times \left( \sum_{b=1}^{5} 3^b \right)$.

Calculate the first sum: $\sum_{a=1}^{5} 2^a = 2^1 + 2^2 + 2^3 + 2^4 + 2^5$. This is a geometric series with first term 2, common ratio 2, and 5 terms. Sum $= \frac{2(2^5 - 1)}{2 - 1} = \frac{2(32 - 1)}{1} = 2 \times 31 = 62$.

Calculate the second sum: $\sum_{b=1}^{5} 3^b = 3^1 + 3^2 + 3^3 + 3^4 + 3^5$. This is a geometric series with first term 3, common ratio 3, and 5 terms. Sum $= \frac{3(3^5 - 1)}{3 - 1} = \frac{3(243 - 1)}{2} = \frac{3 \times 242}{2} = 3 \times 121 = 363$.

The sum of all divisors of N divisible by 6 is the product of these two sums: Sum $= 62 \times 363$. $62 \times 363 = 62 \times (300 + 60 + 3) = 62 \times 300 + 62 \times 60 + 62 \times 3$ $= 18600 + 3720 + 186$ $= 22320 + 186 = 22506$.

The sum of all divisors of 'N' which are divisible by 6 is 22506.

Comparing this value with the given options: (A) 45012 (B) 15246 (C) 22506 (D) 11253

The calculated sum matches option (C).

The final answer is $\boxed{22506}$.

Solution:

1. Calculate the determinant of matrix A: $|A| = 6$.
2. Determine the value of N using the properties of determinants of adjoint and inverse matrices: $N = \frac{|\text{adj. B}|}{|C|} = \frac{|\text{adj. (adj. A)}|}{|A^{-1}|}$. For a 3x3 matrix A, $|\text{adj. (adj. A)}| = |A|^4$ and $|A^{-1}| = \frac{1}{|A|}$. Thus, $N = \frac{|A|^4}{1/|A|} = |A|^5 = 6^5$.
3. Find the prime factorization of N: $N = 6^5 = 2^5 \times 3^5$.
4. Identify the form of divisors of N that are divisible by 6. These are divisors $d = 2^a \times 3^b$ where $1 \le a \le 5$ and $1 \le b \le 5$.
5. Calculate the sum of these divisors. The sum is given by the product of the sum of powers of 2 from $2^1$ to $2^5$ and the sum of powers of 3 from $3^1$ to $3^5$. Sum of powers of 2: $\sum_{a=1}^{5} 2^a = 2+4+8+16+32 = 62$. Sum of powers of 3: $\sum_{b=1}^{5} 3^b = 3+9+27+81+243 = 363$.
6. The required sum is the product of these two sums: $62 \times 363 = 22506$.

The final answer is $\boxed{22506}$.