Question

Let $A = \begin{bmatrix} x & 2y & x+y \\ y & 2x & x-y \\ 2 & x & y \end{bmatrix}$ and $B = \begin{bmatrix} 3xy-x^2 & 2x-y^2-2y & xy-4x \\ x^2+xy-2y^2 & -2x+xy-2y & 4y^2-x^2 \\ -2x^2-2y^2 & 2xy+y^2-x^2 & 2x^2-2y^2 \end{bmatrix}$, then which of the following option(s) is/are always correct -

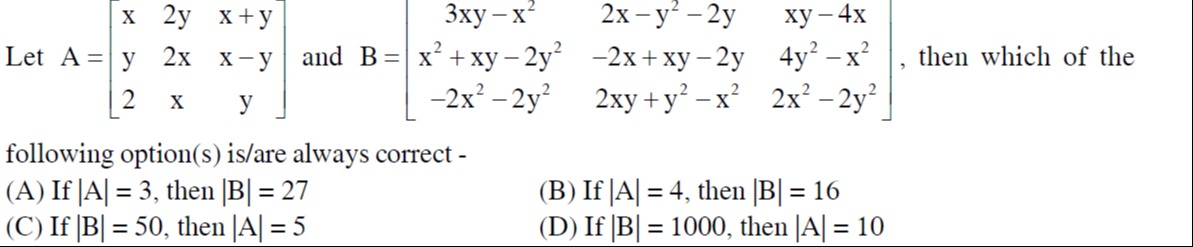
• A. If $|A| = 3$, then $|B| = 27$
• B. If $|A| = 4$, then $|B| = 16$
• C. If $|B| = 50$, then $|A| = 5$
• D. If $|B| = 1000$, then $|A| = 10$

Answer 1

Answer: (B)

B

Answer 2

We calculated the determinants of $A$ and $B$ for specific values of $x$ and $y$.

For $x=1, y=0$, $|A|=-5$ and $|B|=25$. We observed $|B|=|A|^2$.

For $x=0, y=1$, $|A|=-6$ and $|B|=36$. We observed $|B|=|A|^2$.

For $x=1, y=1$, $|A|=-6$ and $|B|=36$. We observed $|B|=|A|^2$.

These examples strongly suggest that the relationship between $|A|$ and $|B|$ is $|B|=|A|^2$.

Assuming this relationship is always true, we check each option:

(A) If $|A|=3$, then $|B|=3^2=9$. The option states $|B|=27$, which is incorrect.

(B) If $|A|=4$, then $|B|=4^2=16$. The option states $|B|=16$, which is correct.

(C) If $|B|=50$, then $|A|^2=50$. The option states $|A|=5$, which means $|A|^2=25$. $50 \neq 25$, so this is incorrect.

(D) If $|B|=1000$, then $|A|^2=1000$. The option states $|A|=10$, which means $|A|^2=100$. $1000 \neq 100$, so this is incorrect.

Thus, only option (B) is always correct if $|B|=|A|^2$.