Question

Let $A = \begin{bmatrix} \sec(x) & \cos(x) & \sec^2(x) + \cot(x)\cdot\csc(x) \\ \cos^2(x) & \cos^2(x) & \csc^2(x) \\ 1 & \cos^2(x) & \cos^2(x) \end{bmatrix}$

Where $x \in (0, \frac{\pi}{2})$, then the value of $|AA^T(A^{-1})^2|$ is (where $|P|$ is determinant value of matrix $P$)

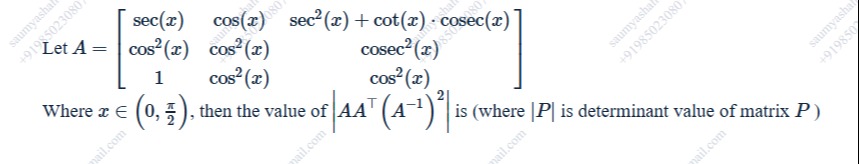
Answer 1

1

Answer 2

Let the given matrix be $A$. We are asked to find the value of $|AA^T(A^{-1})^2|$. Using the properties of determinants:

1. $|AB| = |A||B|$
2. $|A^T| = |A|$
3. $|A^{-1}| = 1/|A|$, provided $|A| \neq 0$.

We can simplify the expression: $|AA^T(A^{-1})^2| = |A| |A^T| |(A^{-1})^2|$ $= |A| |A| |A^{-1}A^{-1}|$ $= |A| |A| |A^{-1}| |A^{-1}|$ $= |A|^2 (1/|A|) (1/|A|)$ $= |A|^2 (1/|A|^2)$ $= 1$

This simplification is valid if $|A| \neq 0$. We need to calculate the determinant of A and check if it is non-zero for $x \in (0, \frac{\pi}{2})$.

We need to confirm that $|A| \neq 0$ for $x \in (0, \pi/2)$. $|A| = \sin^2(x)\cos^3(x) - \sin^2(x) - \cos^3(x)$ For $x \in (0, \pi/2)$, $\sin(x) > 0$ and $\cos(x) > 0$.

Therefore, $|AA^T(A^{-1})^2| = 1$