Question

Let $A = \begin{bmatrix} \omega & -\omega \\ -\omega & \omega \end{bmatrix}$, where $\omega$ is a complex cube root of unity, $B = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$ and $A^9 = 2^kB$, where $k = \dots$

Answer 1

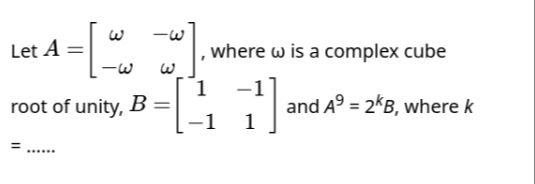
8

Answer 2

To find the value of $k$, we first express matrix $A$ in terms of matrix $B$. Given $A = \begin{bmatrix} \omega & -\omega \\ -\omega & \omega \end{bmatrix}$ and $B = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$. We can factor out $\omega$ from matrix $A$: $A = \omega \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$ So, $A = \omega B$.

Next, we need to find a general expression for $B^n$. Let's calculate the first few powers of $B$: $B^1 = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} = B$

$B^2 = B \cdot B = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$ $B^2 = \begin{bmatrix} (1)(1) + (-1)(-1) & (1)(-1) + (-1)(1) \\ (-1)(1) + (1)(-1) & (-1)(-1) + (1)(1) \end{bmatrix}$ $B^2 = \begin{bmatrix} 1+1 & -1-1 \\ -1-1 & 1+1 \end{bmatrix} = \begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix}$ $B^2 = 2 \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} = 2B$

Now, let's find $B^3$: $B^3 = B^2 \cdot B = (2B) \cdot B = 2B^2$ Since $B^2 = 2B$, we substitute this back: $B^3 = 2(2B) = 4B = 2^2 B$

Let's find $B^4$: $B^4 = B^3 \cdot B = (2^2 B) \cdot B = 2^2 B^2$ Since $B^2 = 2B$, we substitute this back: $B^4 = 2^2(2B) = 2^3 B$

From the pattern, we can generalize that for any positive integer $n \ge 1$: $B^n = 2^{n-1} B$

Now, we need to calculate $A^9$. Since $A = \omega B$, we have: $A^9 = (\omega B)^9$ Since $\omega$ is a scalar, we can write: $A^9 = \omega^9 B^9$

Now, we use the generalized formula for $B^n$ with $n=9$: $B^9 = 2^{9-1} B = 2^8 B$

Substitute this back into the expression for $A^9$: $A^9 = \omega^9 (2^8 B)$

We are given that $\omega$ is a complex cube root of unity. This means $\omega^3 = 1$. We can simplify $\omega^9$: $\omega^9 = (\omega^3)^3 = (1)^3 = 1$

Substitute $\omega^9 = 1$ into the expression for $A^9$: $A^9 = 1 \cdot (2^8 B)$ $A^9 = 2^8 B$

The problem states that $A^9 = 2^kB$. Comparing our result $A^9 = 2^8 B$ with $A^9 = 2^kB$, we can conclude that: $k = 8$