Question

Let $A = \begin{bmatrix} 2 & 1 \\ 1 & 0 \end{bmatrix}^n = (a_{ij}(n))$

If $\lim_{n\to\infty}\frac{a_{12}(n)}{a_{22}(n)} = l$ where $l^2 = \sqrt{a} + \sqrt{b}$

$(a, b \in N)$, find the value of $(a+b)$.

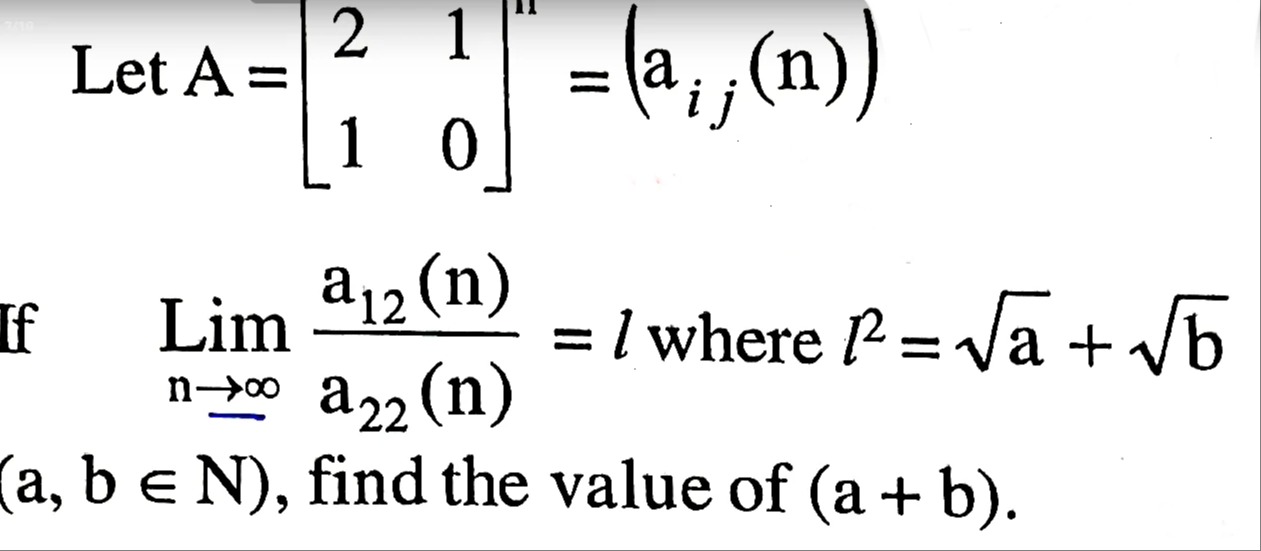
• A. 17
• B. 8
• C. 9
• D. 72

Answer 1

Answer: (A)

17

Answer 2

The characteristic equation of the matrix $M = \begin{bmatrix} 2 & 1 \\ 1 & 0 \end{bmatrix}$ is $\lambda^2 - 2\lambda - 1 = 0$, with eigenvalues $\lambda_1 = 1+\sqrt{2}$ and $\lambda_2 = 1-\sqrt{2}$.

The elements $a_{12}(n)$ and $a_{22}(n)$ can be expressed in terms of these eigenvalues. For $a_{12}(n)$, using the initial conditions $a_{12}(0)=0$ and $a_{12}(1)=1$, we find $a_{12}(n) = \frac{1}{2\sqrt{2}} ((1+\sqrt{2})^n - (1-\sqrt{2})^n)$. For $a_{22}(n)$, using the initial conditions $a_{22}(0)=1$ and $a_{22}(1)=0$, we find $a_{22}(n) = (\frac{1}{2} - \frac{1}{2\sqrt{2}}) (1+\sqrt{2})^n + (\frac{1}{2} + \frac{1}{2\sqrt{2}}) (1-\sqrt{2})^n$.

To find the limit $l = \lim_{n\to\infty}\frac{a_{12}(n)}{a_{22}(n)}$, we divide both the numerator and the denominator by the dominant eigenvalue term $(1+\sqrt{2})^n$: $l = \frac{\lim_{n\to\infty} \frac{a_{12}(n)}{(1+\sqrt{2})^n}}{\lim_{n\to\infty} \frac{a_{22}(n)}{(1+\sqrt{2})^n}} = \frac{\frac{1}{2\sqrt{2}}}{\frac{1}{2} - \frac{1}{2\sqrt{2}}} = \frac{1}{\sqrt{2}-1} = \sqrt{2}+1$.

We are given $l^2 = \sqrt{a} + \sqrt{b}$. $l^2 = (\sqrt{2}+1)^2 = 2 + 2\sqrt{2} + 1 = 3 + 2\sqrt{2}$. So, $3 + 2\sqrt{2} = \sqrt{a} + \sqrt{b}$. By inspection, we can set $\sqrt{a} = 3$ and $\sqrt{b} = 2\sqrt{2}$, or vice versa. This gives $a = 3^2 = 9$ and $b = (2\sqrt{2})^2 = 8$. Alternatively, we can square both sides: $(3 + 2\sqrt{2})^2 = (\sqrt{a} + \sqrt{b})^2$ $9 + 12\sqrt{2} + 8 = a + b + 2\sqrt{ab}$ $17 + 12\sqrt{2} = a + b + 2\sqrt{ab}$. Equating the rational and irrational parts, we get $a+b = 17$ and $2\sqrt{ab} = 12\sqrt{2} \implies ab = 72$. The natural numbers $a$ and $b$ that satisfy $a+b=17$ and $ab=72$ are $8$ and $9$.

Therefore, $a+b = 8+9 = 17$.