Question

Let $A = \begin{bmatrix} 2 & 0 \\ 0 & -3 \end{bmatrix}$, $B = \begin{bmatrix} 0 & 1 \\ 3 & 0 \end{bmatrix}$ and $X = \begin{bmatrix} \cos x & -\sin x \\ \sin x & \cos x \end{bmatrix}$. If $P = AXB, Q = BX^TA$ and $Tr((PQ)^{10}) = a^{10} + b^{10}$, where $a < b$, then value of $(b - 2a)$ is

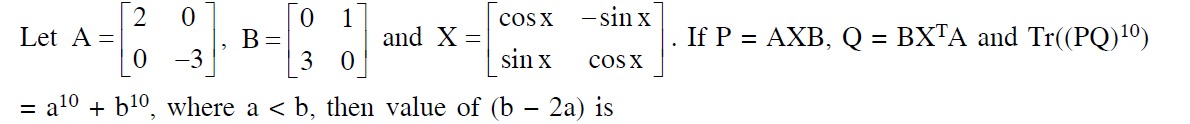
• A. 2
• B. 3
• C. 4
• D. 5

Answer 1

Answer: (B)

3

Answer 2

Here's how to solve the problem:

1. Calculate $B^2$:

   $B^2 = \begin{bmatrix} 0 & 1 \\ 3 & 0 \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 3 & 0 \end{bmatrix} = \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix} = 3I$

2. Note that $X^T = X^{-1}$ since $X$ is a rotation matrix, so $XX^T = X^TX = I$.

3. Simplify $PQ$:

   $PQ = (AXB)(BX^TA) = AX(BB)X^TA = AX(3I)X^TA = 3A(XX^T)A = 3AIA = 3A^2$

4. Calculate $A^2$:

   $A^2 = \begin{bmatrix} 2 & 0 \\ 0 & -3 \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & -3 \end{bmatrix} = \begin{bmatrix} 4 & 0 \\ 0 & 9 \end{bmatrix}$

5. Calculate $PQ$:

   $PQ = 3A^2 = 3\begin{bmatrix} 4 & 0 \\ 0 & 9 \end{bmatrix} = \begin{bmatrix} 12 & 0 \\ 0 & 27 \end{bmatrix}$

6. Calculate $(PQ)^{10}$:

   $(PQ)^{10} = \begin{bmatrix} 12^{10} & 0 \\ 0 & 27^{10} \end{bmatrix}$

7. Calculate $Tr((PQ)^{10})$:

   $Tr((PQ)^{10}) = 12^{10} + 27^{10}$

8. Identify $a$ and $b$:

   Since $a < b$, $a = 12$ and $b = 27$.

9. Calculate $b - 2a$:

   $b - 2a = 27 - 2(12) = 27 - 24 = 3$

Therefore, the value of $b - 2a$ is 3.