Question

Let a be the sum of integer roots of the equation $(x^2 + 4x)^2 - 9(x + 2)^2 = 0$, then the value of $|a|$ is

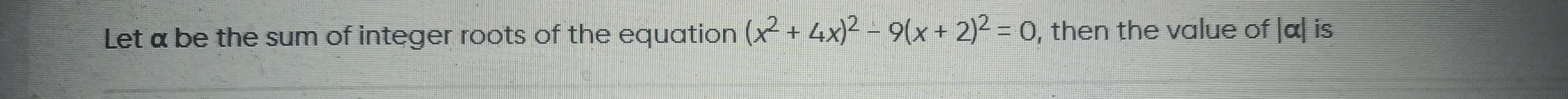
Answer 1

8

Answer 2

The equation $(x^2 + 4x)^2 - 9(x + 2)^2 = 0$ is solved by recognizing it as a difference of squares: $(x^2 + 4x)^2 - (3(x + 2))^2 = 0$. This expands to $(x^2 + 4x - 3(x+2))(x^2 + 4x + 3(x+2)) = 0$.

Simplifying the terms gives two quadratic equations:

1. $x^2 + x - 6 = 0 \implies (x+3)(x-2) = 0 \implies x = -3, 2$.
2. $x^2 + 7x + 6 = 0 \implies (x+1)(x+6) = 0 \implies x = -1, -6$.

All roots are integers. The sum of these integer roots is $a = (-3) + 2 + (-1) + (-6) = -8$.

The value of $|a|$ is $|-8| = 8$.