Question

Let $A$ be the set of all lines in a plane and let $R$ be a relation in $A$ defined by R=\left\\{ \left( {{L}_{1}},{{L}_{2}} \right):{{L}_{1}}\bot {{L}_{2}} \right\\} . Show that $R$ is symmetric but neither reflexive nor transitive.

Answer 1

Hint:For solving this question we will consider some suitable geometrical figures for proving that relation R=\left\\{ \left( {{L}_{1}},{{L}_{2}} \right):{{L}_{1}}\bot {{L}_{2}} \right\\} is symmetric but neither reflexive nor transitive separately.

Complete step-by-step answer:
Given:
It is given that there is a set $A$ of all lines in a plane and let $R$ be a relation in $A$ , defined by R=\left\\{ \left( {{L}_{1}},{{L}_{2}} \right):{{L}_{1}}\bot {{L}_{2}} \right\\} and we have to prove that $R$ is symmetric but neither reflexive nor transitive.
Now, we will prove that the given relation is symmetric but neither reflexive nor transitive one by one.
1. If ${{L}_{1}}={{L}_{2}}$ where ${{L}_{1}}$ is any line in a plane form the set $A$ then it is obvious that a line cannot be perpendicular to itself. Now, we can conclude that $\left( {{L}_{1}},{{L}_{1}} \right)\notin R$ where ${{L}_{1}}$ is any line in a plane form the set $A$ . Thus, the given relation is not reflexive.

2. If ${{L}_{1}}$ and ${{L}_{2}}$ are two different lines in a plane form the set $A$ such that ${{L}_{1}}\bot {{L}_{2}}$ so, $\left( {{L}_{1}},{{L}_{2}} \right)\in R$ . Then, it is always necessary that ${{L}_{2}}\bot {{L}_{1}}$ and we can see this with the help of the figure given below:

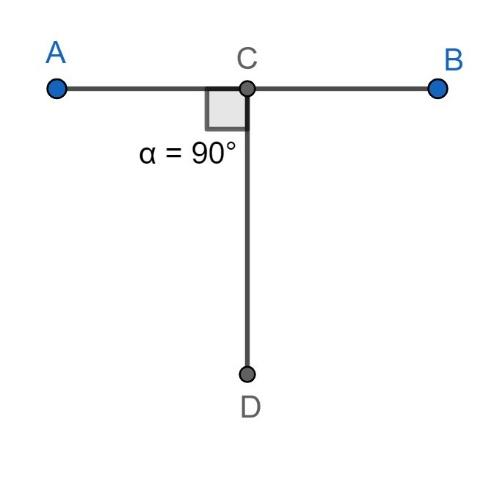
In the above figure, we can say that both segments AB and CD are perpendicular to each other. Now, we can conclude that if $\left( {{L}_{1}},{{L}_{2}} \right)\in R$ then we can say that $\left( {{L}_{2}},{{L}_{1}} \right)\in R$ always. Thus, if $\left( {{L}_{1}},{{L}_{2}} \right)\in R$ then $\left( {{L}_{2}},{{L}_{1}} \right)\in R$ so, the given relation is symmetric.
3. If ${{L}_{1}}$ , ${{L}_{2}}$ and ${{L}_{3}}$ are three different lines in a plane form the set $A$ such that ${{L}_{1}}\bot {{L}_{2}}$ and ${{L}_{2}}\bot {{L}_{3}}$ so, $\left( {{L}_{1}},{{L}_{2}} \right)\in R$ and $\left( {{L}_{2}},{{L}_{3}} \right)\in R$ . Then, it is not true that ${{L}_{1}}\bot {{L}_{3}}$ and we can see this with the help of the figure given below:

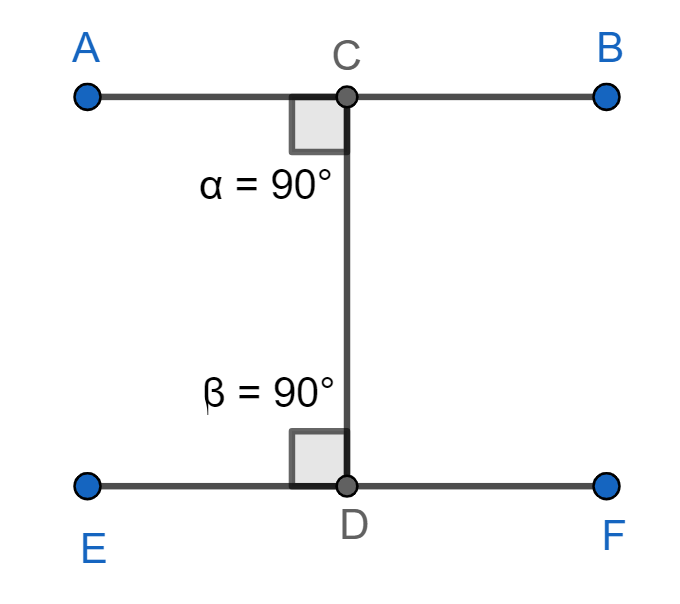
In the above figure, we can say that both segments AB is perpendicular to CD and CD is perpendicular to EF but it is not true that AB is perpendicular to EF instead of that AB will be parallel to EF. Now, we conclude that if $\left( a,b \right)\in R$ and $\left( b,c \right)\in R$ then, it is not true that $\left( a,c \right)\in R$ . Thus, if $\left( a,b \right)\in R$ and $\left( b,c \right)\in R$ then $\left( a,c \right)\notin R$ so, the given relation is not transitive.
Now, as we have proved that the given relation is symmetric but neither reflexive nor transitive.
Hence, proved.

Note: Here, the student must try to understand the relation given in the problem then prove that the relation is symmetric but neither reflexive nor transitive separately and don’t mix up their conditions with each other to avoid the confusion. Moreover, we should understand with the help of suitable geometrical figures for better clarity of the concept.