Question

Let $A$ be a square matrix which satisfies

$A^2 - A + 2I = 0$ and

$A^4 + A^8 + A^{10} = aA + bI$. Then $a + b =$(where $I$ is Identity Matrix, Order of matrix $I$ and Order of matrix $A$ are same)

Answer 1

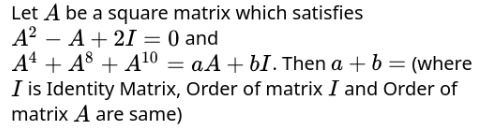
5

Answer 2

The problem requires us to express higher powers of matrix $A$ in terms of $A$ and $I$ using the given matrix equation $A^2 - A + 2I = 0$.

Given:

1. $A^2 - A + 2I = 0$
2. $A^4 + A^8 + A^{10} = aA + bI$

From the first equation, we can write $A^2$ as:

$A^2 = A - 2I \quad \cdots (1)$

Now, we calculate $A^4$, $A^8$, and $A^{10}$ in terms of $A$ and $I$.

1. Calculate $A^4$:

$A^4 = (A^2)^2$

Substitute $A^2$ from (1):

$A^4 = (A - 2I)^2$

$A^4 = A^2 - 2(A)(2I) + (2I)^2$

$A^4 = A^2 - 4AI + 4I^2$

Since $AI = A$ and $I^2 = I$:

$A^4 = A^2 - 4A + 4I$

Substitute $A^2$ from (1) again:

$A^4 = (A - 2I) - 4A + 4I$

$A^4 = A - 2I - 4A + 4I$

$A^4 = -3A + 2I \quad \cdots (2)$

2. Calculate $A^8$:

$A^8 = (A^4)^2$

Substitute $A^4$ from (2):

$A^8 = (-3A + 2I)^2$

$A^8 = (-3A)^2 + 2(-3A)(2I) + (2I)^2$

$A^8 = 9A^2 - 12AI + 4I^2$

$A^8 = 9A^2 - 12A + 4I$

Substitute $A^2$ from (1):

$A^8 = 9(A - 2I) - 12A + 4I$

$A^8 = 9A - 18I - 12A + 4I$

$A^8 = -3A - 14I \quad \cdots (3)$

3. Calculate $A^{10}$:

$A^{10} = A^8 \cdot A^2$

Substitute $A^8$ from (3) and $A^2$ from (1):

$A^{10} = (-3A - 14I)(A - 2I)$

$A^{10} = (-3A)(A) + (-3A)(-2I) + (-14I)(A) + (-14I)(-2I)$

$A^{10} = -3A^2 + 6AI - 14IA + 28I^2$

Since $AI = A$, $IA = A$, and $I^2 = I$:

$A^{10} = -3A^2 - 8A + 28I$

Substitute $A^2$ from (1):

$A^{10} = -3(A - 2I) - 8A + 28I$

$A^{10} = -3A + 6I - 8A + 28I$

$A^{10} = -11A + 34I \quad \cdots (4)$

4. Substitute into the second given equation:

Now, substitute the expressions for $A^4$, $A^8$, and $A^{10}$ from (2), (3), and (4) into the equation $A^4 + A^8 + A^{10} = aA + bI$:

$(-3A + 2I) + (-3A - 14I) + (-11A + 34I) = aA + bI$

Combine the terms with $A$ and the terms with $I$:

$(-3 - 3 - 11)A + (2 - 14 + 34)I = aA + bI$

$(-17)A + (22)I = aA + bI$

5. Compare coefficients:

By comparing the coefficients of $A$ and $I$ on both sides, we get:

$a = -17$

$b = 22$

6. Calculate $a+b$:

$a + b = -17 + 22 = 5$

The final answer is $\boxed{5}$.

Explanation of the solution:

The core idea is to repeatedly use the given matrix relation $A^2 = A - 2I$ to reduce any higher power of $A$ into a linear combination of $A$ and $I$.

1. Express $A^2$ in terms of $A$ and $I$.
2. Calculate $A^4 = (A^2)^2$, substituting $A^2$ and simplifying to the form $k_1 A + k_2 I$.
3. Calculate $A^8 = (A^4)^2$, substituting $A^4$ and simplifying to the form $k_3 A + k_4 I$.
4. Calculate $A^{10} = A^8 \cdot A^2$, substituting $A^8$ and $A^2$ and simplifying to the form $k_5 A + k_6 I$.
5. Sum the simplified expressions for $A^4$, $A^8$, and $A^{10}$.
6. Equate the resulting expression to $aA + bI$ and compare coefficients to find $a$ and $b$.
7. Compute $a+b$.