Question
Question: Let A be a square matrix satisfying $A^2=2I$ and $\sum_{k=1}^{2n} A^k=63A(A+I)$, then the value of n...
Let A be a square matrix satisfying A2=2I and ∑k=12nAk=63A(A+I), then the value of n
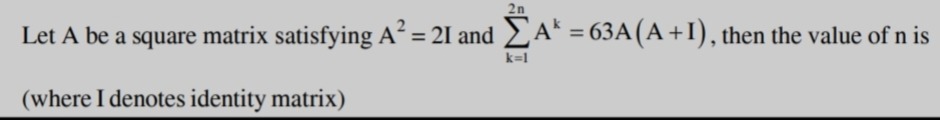
5
6
7
8
6
Solution
Given the matrix equation A2=2I. We need to evaluate the sum ∑k=12nAk. The powers of A can be determined as follows: A1=A A2=2I A3=A2⋅A=2I⋅A=2A A4=A2⋅A2=(2I)(2I)=4I A5=A4⋅A=4I⋅A=4A A6=A4⋅A2=(4I)(2I)=8I
In general, for odd k, Ak=2(k−1)/2A. For even k, Ak=2k/2I.
Now, let's split the sum into odd and even powers: ∑k=12nAk=(A1+A3+⋯+A2n−1)+(A2+A4+⋯+A2n)
Sum of odd powers: A1+A3+⋯+A2n−1=A+2A+4A+⋯+2n−1A =A(1+2+4+⋯+2n−1) This is a geometric series with first term 1, ratio 2, and n terms. The sum is 1⋅2−12n−1=2n−1. So, the sum of odd powers is A(2n−1).
Sum of even powers: A2+A4+⋯+A2n=2I+4I+8I+⋯+2nI =I(2+4+8+⋯+2n) This is a geometric series with first term 2, ratio 2, and n terms. The sum is 2⋅2−12n−1=2(2n−1). So, the sum of even powers is 2I(2n−1).
Therefore, ∑k=12nAk=A(2n−1)+2I(2n−1)=(2n−1)(A+2I).
Now consider the right side of the given equation: 63A(A+I). 63A(A+I)=63(A2+A) Since A2=2I, we substitute this into the expression: 63(2I+A)=63(A+2I).
Equating the left and right sides of the given equation: (2n−1)(A+2I)=63(A+2I).
To solve for n, we need to consider if (A+2I) is invertible. The eigenvalues of A satisfy λ2=2, so λ=±2. The eigenvalues of A+2I are λ+2, which are 2+2 and −2+2. Since these eigenvalues are non-zero, the matrix A+2I is invertible.
We can divide both sides of the equation by (A+2I): 2n−1=63 2n=63+1 2n=64 2n=26 Therefore, n=6.
The value of n is 6.
