Question

Let a, b, c and d be the position vectors of A, B, C and D respectively which are the vertices of a tetrahedron. Then prove that the line joining the vertices to the centroids of the opposite faces are concurrent (this point is called the centroid or the centre of the tetrahedron).

Answer 1

1. First find the position vectors of the centroids of all the four faces of the tetrahedron.
As we know, the centroid of a triangle divides its any median in the ratio of 2:1.
From here we can find its position vector easily using the section formula.
2. Now, we know that the centroid (centre) of a tetrahedron divides the line from any vertex to the centroid of the opposite face in the ratio of 3:1.
So, its position vector can also be found using the section formula.
Find the position vector of the centre of the tetrahedron by applying section formula on all the four lines, it will come out to be the same.
Formula used:
Section formulae: If A and B are two points with position vectors $\vec a$ and $\vec b$ respectively, and let C be a point dividing AB internally in the ratio m:n. Then the position vector of C is given by:
$\vec c = \dfrac{{m\vec b + n\vec a}}{{m + n}}$

Complete step by step solution:
First of all, we need to learn how to write the position vector of a centroid of a triangle in terms of the position vectors of its vertices.
Let us assume a triangle ABC with position vectors of the vertices being $\vec a$, $\vec b$ and $\vec c$ respectively.

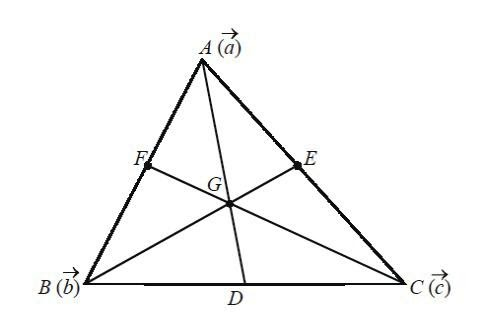
As we know, that the median from the vertex of a triangle bisects the opposite side of the triangle.
Therefore, D is the midpoint of side BC.

Then the position vector of point D will be given by:
$\vec d = \dfrac{{\vec b + \vec c}}{2}$

Now, we also know that the centroid of a triangle divides any of its median in the ratio of 2:1.
Hence, we can say that the point G divides the median Ad in the ratio of 2:1.
$\Rightarrow AG:GD = 2:1$

From section formula the position vector of centroid G is found to be:
$\overrightarrow {OG} = \dfrac{{2\left( {\vec d} \right) + 1\left( {\vec a} \right)}}{{2 + 1}} \\\ \Rightarrow \overrightarrow {OG} = \dfrac{{2\left( {\dfrac{{\vec b + \vec c}}{2}} \right) + \vec a}}{3} \\\ \Rightarrow \overrightarrow {OG} = \dfrac{{\vec a + \vec b + \vec c}}{3} \\\$
Let ABCD be a tetrahedron. And the position vectors of the vertices A, B, C and D be $\vec a$, $\vec b$, $\vec c$ and $\vec d$ respectively.

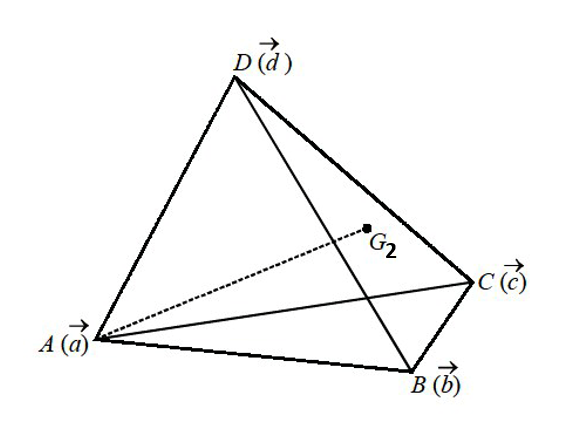
Let $G,{G_1},{G_2},{G_3}$be the centroid of the faces ABC, ABD, BCD and CAD respectively.
Then,
Position vector of $G = \dfrac{{\vec a + \vec b + \vec c}}{3}$
Position vector of ${G_1} = \dfrac{{\vec a + \vec b + \vec d}}{3}$
Position vector of ${G_2} = \dfrac{{\vec b + \vec c + \vec d}}{3}$
Position vector of ${G_3} = \dfrac{{\vec c + \vec a + \vec d}}{3}$

Now, it is to be noted that the centroid of the tetrahedron divides any of the lines $AG,B{G_1},C{G_2},D{G_3}$internally in the ratio of 3:1.
Therefore, finding:

Position vector of a point dividing DG in the ratio of 3:1: -
$= \dfrac{{3\left( {\dfrac{{\vec a + \vec b + \vec c}}{3}} \right) + 1\left( {\vec d} \right)}}{{3 + 1}} \\\ = \dfrac{{\vec a + \vec b + \vec c + \vec d}}{4} \\\$
Position vector of a point dividing $A{G_2}$ in the ratio of 3:1: -
$= \dfrac{{3\left( {\dfrac{{\vec b + \vec c + \vec d}}{3}} \right) + 1\left( {\vec a} \right)}}{{3 + 1}} \\\ = \dfrac{{\vec a + \vec b + \vec c + \vec d}}{4} \\\$

Position vector of a point dividing $B{G_3}$in the ratio of 3:1: -
$= \dfrac{{3\left( {\dfrac{{\vec c + \vec a + \vec d}}{3}} \right) + 1\left( {\vec b} \right)}}{{3 + 1}} \\\ = \dfrac{{\vec a + \vec b + \vec c + \vec d}}{4} \\\$
Position vector of a point dividing $C{G_1}$ in the ratio of 3:1: -
$= \dfrac{{3\left( {\dfrac{{\vec a + \vec b + \vec d}}{3}} \right) + 1\left( {\vec c} \right)}}{{3 + 1}} \\\ = \dfrac{{\vec a + \vec b + \vec c + \vec d}}{4} \\\$
Thus, the point having position vector $\dfrac{{\vec a + \vec b + \vec c + \vec d}}{4}$ is common to $DG,A{G_2},B{G_3}{\text{ and }}C{G_1}$.
Hence, the line joining the vertices of a tetrahedron to the centroids of the opposite faces are concurrent.

Note:
The position vector of the centroid of a triangle ABC with position vectors of the vertices being $\vec a$, $\vec b$ and $\vec c$ respectively is given by:
$\overrightarrow {OG} = \dfrac{{\vec a + \vec b + \vec c}}{3}$

The position vector of the centroid of a tetrahedron ABC with position vectors of the vertices being $\vec a$, $\vec b$, $\vec c$ and $\vec d$ respectively is given by:
$\dfrac{{\vec a + \vec b + \vec c + \vec d}}{4}$