Question

Let A and B be two non-singular matrices of order 3 x 3. $B^{-1}A^{2}B + B = 0$ and determinant of matrix B is $\frac{1}{2}$ then det($C^{-1}$) equals (where $C = A^{2}B^{2} + B^{3} + A^{4}$)

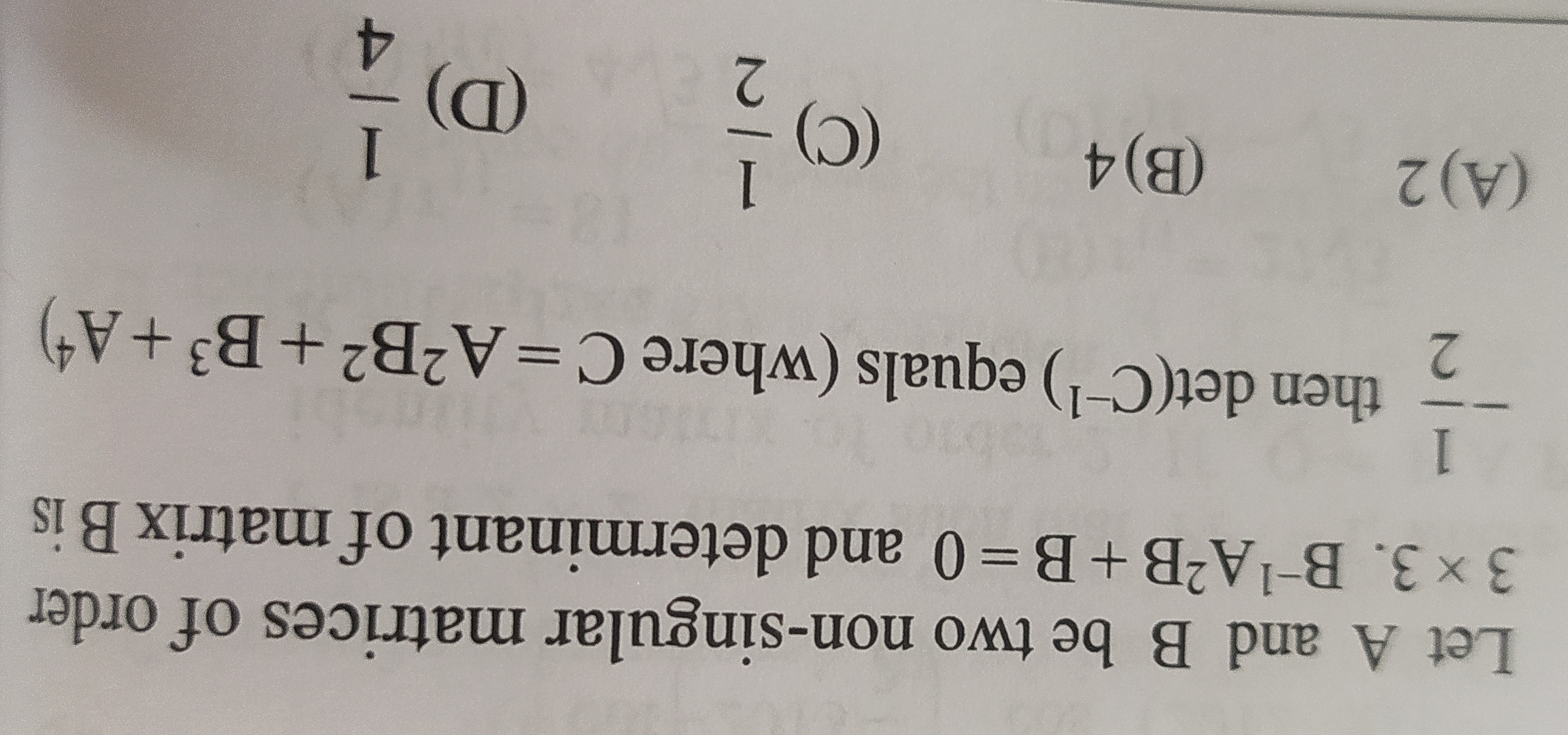
• A. 2
• B. 4
• C. $\frac{1}{2}$
• D. $\frac{1}{4}$

Answer 1

Answer: (B)

4

Answer 2

The given equation is $B^{-1}A^{2}B + B = 0$. Since B is a non-singular matrix, $B^{-1}$ exists. Multiply the equation by B on the left:

$B(B^{-1}A^{2}B + B) = B \cdot 0$ $(BB^{-1})A^{2}B + B^2 = 0$ $IA^{2}B + B^2 = 0$ (where I is the identity matrix) $A^{2}B = -B^2$

Since B is non-singular, $B^2$ is also non-singular. We can multiply the equation $A^{2}B = -B^2$ by $B^{-1}$ on the right:

$A^{2}B B^{-1} = -B^2 B^{-1}$ $A^{2}I = -B(B B^{-1})$ $A^2 = -BI$ $A^2 = -B$

Now consider the expression for C: $C = A^{2}B^{2} + B^{3} + A^{4}$ Substitute $A^2 = -B$ into this expression. $C = (-B)B^2 + B^3 + (A^2)^2$ $C = -B^3 + B^3 + (-B)^2$ $C = 0 + B^2$ $C = B^2$

We need to find det($C^{-1}$). Since $C = B^2$, we have $C^{-1} = (B^2)^{-1}$. Using the property $(M^n)^{-1} = (M^{-1})^n$, we get $(B^2)^{-1} = (B^{-1})^2$. So, $C^{-1} = (B^{-1})^2$.

Now, calculate the determinant of $C^{-1}$: det($C^{-1}$) = det($(B^{-1})^2$) Using the property det($M^n$) = (det(M))^n, we get: det($(B^{-1})^2$) = (det($B^{-1}$))^2

We know that for a non-singular matrix B, det($B^{-1}$) = 1/det(B). We are given that det(B) = 1/2. So, det($B^{-1}$) = 1 / (1/2) = 2.

Substitute this value back into the expression for det($C^{-1}$): det($C^{-1}$) = (det($B^{-1}$))^2 = $2^2 = 4$.

Therefore, the final answer is 4.