Question
Question: Let A and B be two independent events such that $\mathbb{P}(\overline{A}/\overline{B}) = \frac{2}{3...
Let A and B be two independent events such that
P(A/B)=32 then P(A∩B)
P(1)+P(2)=21,
equals
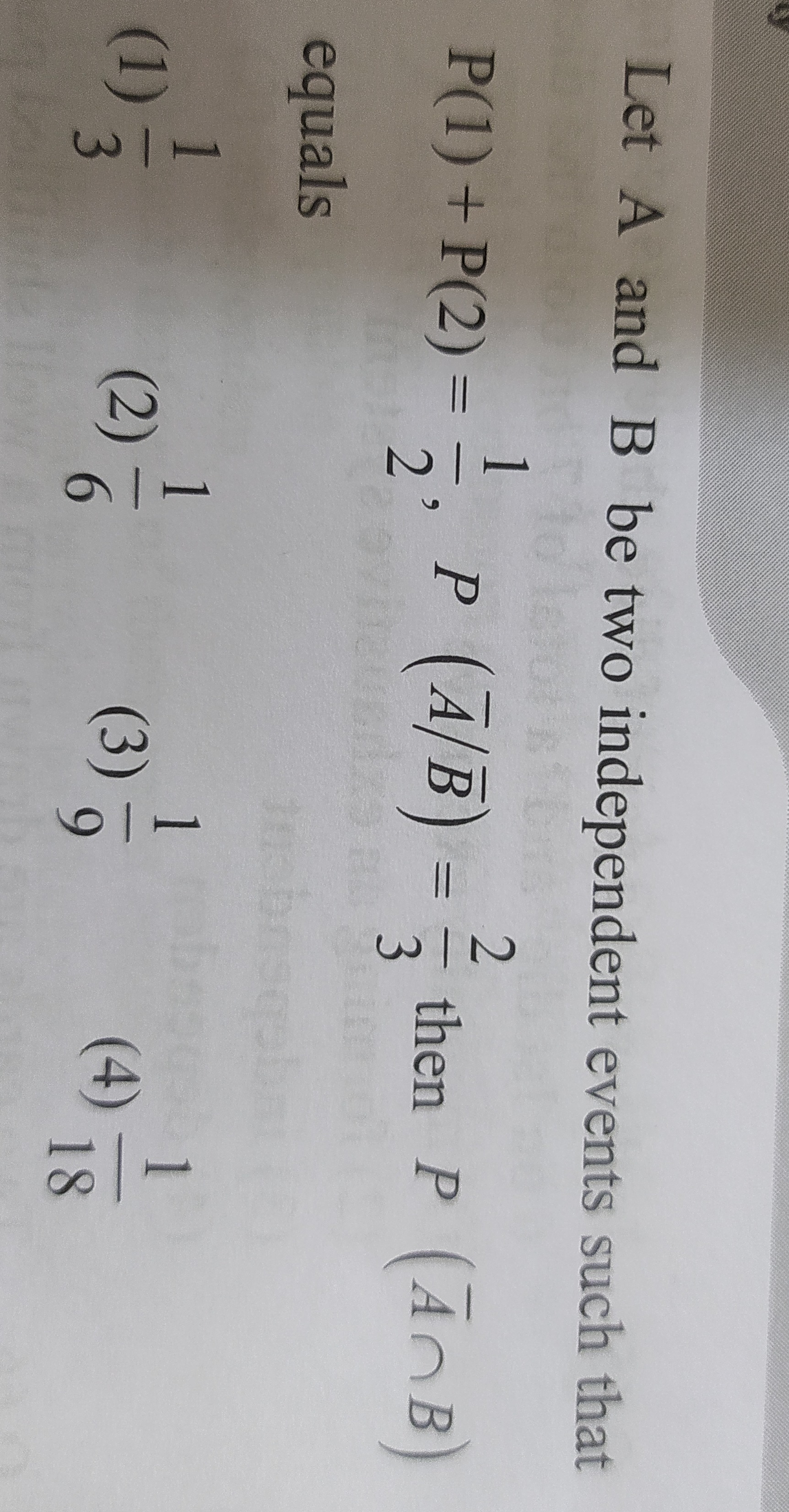
31
61
91
181
61
Solution
Let A and B be two independent events. We are given P(A/B)=32. Since A and B are independent, their complements A and B are also independent. For independent events, the conditional probability P(A/B) is equal to the marginal probability P(A). So, P(A)=32. The probability of event A is P(A)=1−P(A)=1−32=31.
The second condition given is "P(1)+P(2)=21". This notation is unusual in the context of events A and B. Assuming this is a typo and it refers to the probability of the union of events A and B, the condition is interpreted as P(A∪B)=21.
For any two events A and B, the probability of their union is given by P(A∪B)=P(A)+P(B)−P(A∩B). Since A and B are independent, the probability of their intersection is P(A∩B)=P(A)P(B). Substituting this into the union formula, we get P(A∪B)=P(A)+P(B)−P(A)P(B).
We have P(A)=31 and assumed P(A∪B)=21. Let P(B)=p.
21=31+p−31p
21=31+p(1−31)
21=31+p(32)
Subtract 31 from both sides:
21−31=32p
63−2=32p
61=32p
Solve for p:
p=61×23=123=41.
So, P(B)=41.
We need to find P(A∩B). Since A and B are independent events, A and B are also independent events. The probability of the intersection of independent events A and B is the product of their individual probabilities:
P(A∩B)=P(A)P(B).
We found P(A)=32 and P(B)=41.
P(A∩B)=32×41=122=61.
