Question

Let A and B be two distinct points on the parabola ${y^2} = 4x$ . If the axis of the parabola touches a circle of radius $2$ having AB as its diameter , then the slope of the line joining A and B can be
$\left( 1 \right) - \left( {\dfrac{1}{2}} \right)$
$\left( 2 \right)\dfrac{1}{2}$
$\left( 3 \right)1$
$\left( 4 \right)$ None of these

Answer 1

In order to solve this question, we must be familiar with parabola, an integral part of conic sections. A parabola is a curve where any point is at an equal distance from focus ( a fixed point ) and a fixed straight line which is called a directrix. The standard and simplest equation for a parabola is ${y^2} = 4ax$ , when the directrix is parallel to the y-axis. To represent a point on a parabola, parametric coordinates are used and are given by $\left( {a{t^2},2at} \right)$ where t is a parameter, these coordinates always satisfy the equation of the parabola.

Complete step by step answer:
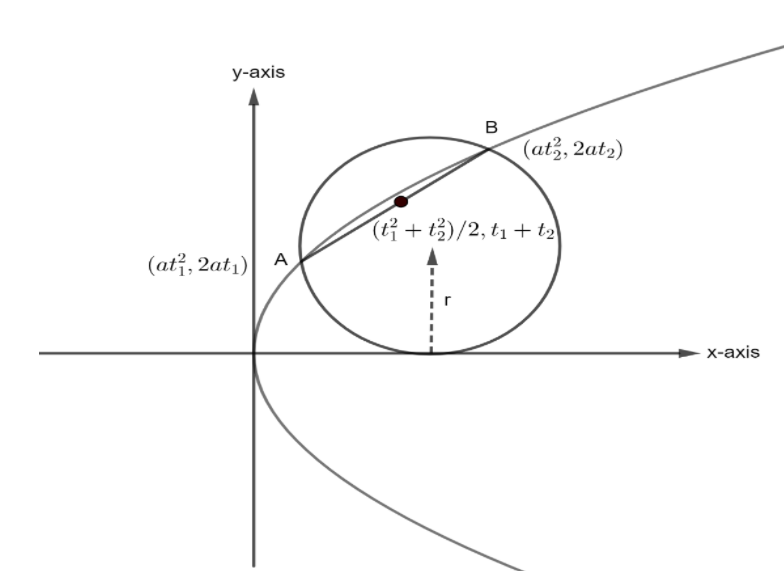
The above question is represented diagrammatically in figure below.
Given: ${y^2} = 4x$
Compared with the standard equation for parabola i.e. ${y^2} = 4ax$ , we can say that the value of $a = 1$ .
The axis of the parabola touches a circle of radius $= 2$ , the circle’s diameter is given as AB.
We can calculate any point on the parabola, using the parametric coordinates i.e. $\left( {a{t^2},2at} \right)$
The parametric co-ordinates of point A are given by ;
$\Rightarrow \left( {{t_1}^2,2{t_1}} \right)$ $\left( {\because a = 1} \right)$
Similarly, the parametric co-ordinates of point B are given by ;
$\Rightarrow \left( {{t_2}^2,2{t_2}} \right)$ $\left( {\because a = 1} \right)$
According to the given question, we have to calculate the slope of the line joining point A and point B ;
The mid-point of the line joining A and B can be calculated as ;

$\left[ {\because {\text{midpoint = }}\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right]$
Using the formula stated above, we get the midpoint as ;
$\Rightarrow {\text{midpoint = }}\left( {\dfrac{{{t_1}^2 + {t_2}^2}}{2},\dfrac{{2\left( {{t_1} + {t_2}} \right)}}{2}} \right)$
On further simplification;
$\Rightarrow {\text{midpoint = }}\left( {\dfrac{{{t_1}^2 + {t_2}^2}}{2},{\text{ }}{t_1} + {t_2}} \right){\text{ }}......\left( 1 \right)$
The axis of the parabola is x-axis and the circle touches the x-axis. Therefore, the distance of midpoint from the x axis $=$ Radius of the circle .
We know that the radius of the circle is $r = 2$ ;
Therefore, comparing the two terms;
$\Rightarrow {t_1} + {t_2} = 2{\text{ }}......\left( 2 \right)$
The slope of line segment joining AB is given by ;
$\left[ {\because {\text{Slope = }}\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right]$
Using the above formula for point A and point B , we get;
$\Rightarrow {\text{Slope}} = \dfrac{{2{t_2} - 2{t_1}}}{{{t_2}^2 - {t_1}^2}}$
By the algebraic identity;
${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$
$\Rightarrow \dfrac{{2\left( {{t_2} - {t_1}} \right)}}{{\left( {{t_1} + {t_2}} \right)\left( {{t_2} - {t_1}} \right)}} = \dfrac{2}{{{t_1} + {t_2}}}$
From equation $\left( 2 \right)$ , we know that ${t_1} + {t_2} = 2{\text{ }}$ ;
$\Rightarrow \dfrac{2}{{{t_1} + {t_2}}} = \dfrac{2}{2} = 1$

So, the correct answer is “Option 3”.

Note:
To solve such types of questions, the parametric coordinates of the parabola should be used. The parametric coordinates of a parabola are easier to deal with. If ${y^2} = 4ax$ is standard equation of parabola and P and Q are the end points of any focal chord then $P\left( {a{t_1}^2,2a{t_1}} \right){\text{ and Q}}\left( {a{t_2}^2,2a{t_2}} \right)$ represents the parametric coordinates. Firstly, draw the correct and proper diagram according to the given question then find the center of the circle. By using the coordinates of center, and the formula for slope of a line we will get the required solution.