Question

Let A = $[a_{ij}]_{2 \times 2}$ where $a_{ij} \neq 0$ for all i, j and $A^2 = I$. Let a be the sum of all diagonal elements of A and $b = |A|$, then $\frac{90a^2 + 16b^2}{3}$ is equal to

Answer 1

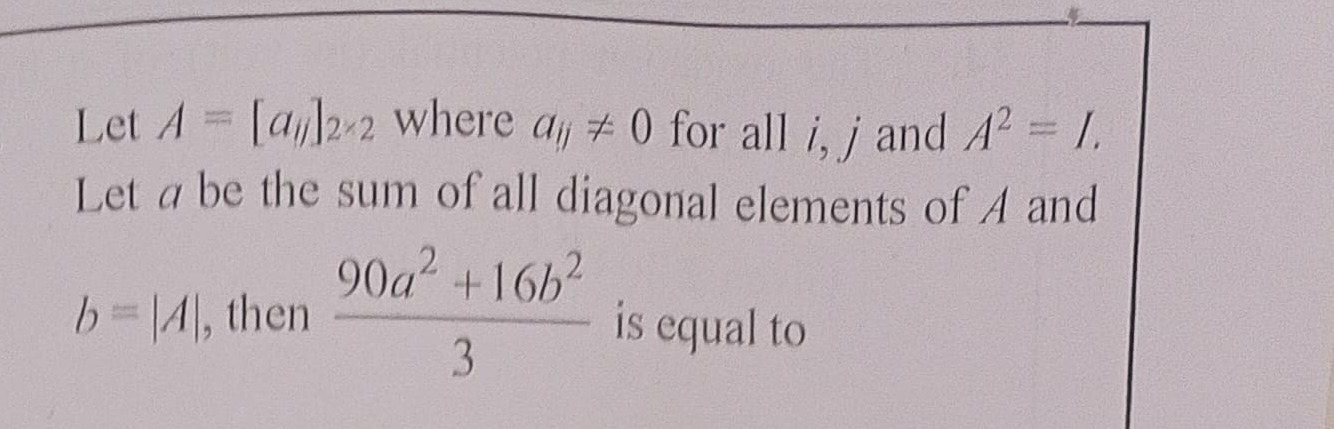
16/3

Answer 2

Let the matrix A be $A = \begin{bmatrix} p & q \\ r & s \end{bmatrix}$. Given that $a_{ij} \neq 0$ for all i, j, it implies $p, q, r, s \neq 0$.

The sum of all diagonal elements of A is $a = p+s$. The determinant of A is $b = |A| = ps - qr$.

We are given the condition $A^2 = I$, where $I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ is the identity matrix. Let's compute $A^2$: $A^2 = \begin{bmatrix} p & q \\ r & s \end{bmatrix} \begin{bmatrix} p & q \\ r & s \end{bmatrix} = \begin{bmatrix} p^2+qr & pq+qs \\ rp+sr & rq+s^2 \end{bmatrix}$.

Equating $A^2$ to $I$: $\begin{bmatrix} p^2+qr & pq+qs \\ rp+sr & rq+s^2 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$.

From this matrix equality, we get a system of equations:

1. $p^2+qr = 1$
2. $pq+qs = 0 \implies q(p+s) = 0$
3. $rp+sr = 0 \implies r(p+s) = 0$
4. $rq+s^2 = 1$

From equation (2), since $q \neq 0$ (given $a_{ij} \neq 0$), we must have $p+s = 0$. This implies $s = -p$.

Let's verify this with equation (3). Since $r \neq 0$ (given $a_{ij} \neq 0$), we also get $p+s=0$, which is consistent.

Now we can find the value of 'a': $a = p+s = 0$.

Next, let's find the value of 'b'. $b = ps - qr$. Substitute $s = -p$ into the expression for 'b': $b = p(-p) - qr = -p^2 - qr$.

From equation (1), we have $p^2+qr = 1$. We can rewrite this as $qr = 1 - p^2$.

Substitute $qr = 1 - p^2$ into the expression for 'b': $b = -p^2 - (1 - p^2)$ $b = -p^2 - 1 + p^2$ $b = -1$.

So, we have $a=0$ and $b=-1$.

Finally, we need to calculate the value of $\frac{90a^2 + 16b^2}{3}$. Substitute the values of 'a' and 'b': $\frac{90(0)^2 + 16(-1)^2}{3}$ $= \frac{90(0) + 16(1)}{3}$ $= \frac{0 + 16}{3}$ $= \frac{16}{3}$.

The condition $a_{ij} \neq 0$ is essential. For example, if $p=1$, then $s=-1$. From $p^2+qr=1$, we get $1^2+qr=1$, which means $qr=0$. This would imply $q=0$ or $r=0$, contradicting the condition $a_{ij} \neq 0$. Thus, $p$ cannot be $1$ or $-1$. For instance, if $p=2$, then $s=-2$. Then $qr = 1-p^2 = 1-4 = -3$. We can choose $q=1$ and $r=-3$. This gives $A = \begin{bmatrix} 2 & 1 \\ -3 & -2 \end{bmatrix}$, which satisfies all given conditions. For this matrix, $a=2+(-2)=0$ and $b=(2)(-2)-(1)(-3)=-4+3=-1$, confirming our derived values for 'a' and 'b'.

The final answer is $\boxed{\frac{16}{3}}$.

Explanation of the solution:

1. Represent the matrix A as $\begin{bmatrix} p & q \\ r & s \end{bmatrix}$.
2. Use the condition $A^2=I$ to set up equations for the elements $p, q, r, s$.
3. From the off-diagonal elements, $q(p+s)=0$ and $r(p+s)=0$. Since $q, r \neq 0$, it implies $p+s=0$.
4. This directly gives $a = p+s = 0$.
5. From the diagonal elements, $p^2+qr=1$.
6. Calculate $b=|A|=ps-qr$. Substitute $s=-p$ and $qr=1-p^2$ into the expression for $b$.
7. This yields $b = p(-p) - (1-p^2) = -p^2 - 1 + p^2 = -1$.
8. Substitute $a=0$ and $b=-1$ into the given expression $\frac{90a^2 + 16b^2}{3}$ to get the final value.